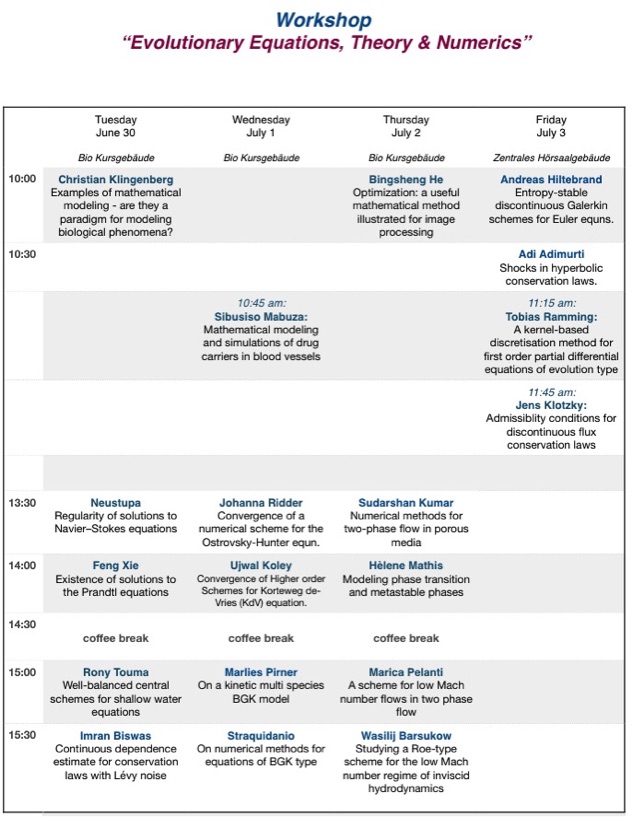
WORKSHOP: EVOLUTIONARY EQUATIONS, THEORY AND NUMERICS

Titles and abstracts:
Adi Adimurthi (Tata Institute, Bangalore, India)
Title : Shocks in Hyperbolic conservation laws.
Abstract : Shocks are natural phenomena and mathematical understanding is wide open. In this talk I will describe how different types of stable shocks occur in the mathematical theory of conservation laws.
Wasilj Barsukow (Würzburg University)
Title : Studying a Roe-type scheme for the low Mach number regime of inviscid hydrodynamics
Abstract :
The limit of small Mach numbers for compressible Euler equations is, upon suitable initial conditions, described by the equations of incompressible hydrodynamics. Often, the validity of simulations (e.g. in astrophysics) depends crucially on the ability to resolve this regime. Without special effort, Roe-type schemes are typically found to be increasingly diffusive in the limit of low Mach numbers, often deteriorating the results in an unacceptable manner. Modifying this upwind matrix (e.g. via so-called preconditioning) has turned out to be a successful method to obtain a Mach number independent diffusion. However this change may have consequences for the stability of the method. We present the new preconditioner (Miczek et. al. 2015) and study its asymptotic properties and stability.
Imran Biswas (Tata Institute, Bangalore, India)
Title : Continuous dependence estimate for conservation laws with Lévy noise
Abstract :
We are concerned with multidimensional stochastic balance laws driven by Le ́vy processes. Using bounded variation (BV) estimates for vanishing viscosity approximations, we derive an explicit continuous depen- dence estimate on the nonlinearities of the entropy solutions under the assumption that Le ́vy noise only depends on the solution. This result is used to show the error estimate for the stochastic vanishing viscosity method. In addition, we establish fractional BV estimate for vanishing viscosity approximations in case the noise coefficient depends on both the solution and spatial variable.
Cleopatra Christoforou (University of Cyprus in Nicosia)
unfortunately she had to cancel her attendance
Bingsheng He (Nanjing University, Nanjing, China)
Title : Optimization: a useful mathematical method illustrated for image processing
Abstract :
I will give a general introduction into a mathematical method called "mathematical optimization”. This method is able to find the best solution to a problem which is described in a certain mathematical language. Among other examples I will illustrate how in image processing this method is able to improved digital images.
Andreas Hiltebrand (ETH-Zürich, Switzerland)
Title: Entropy-stable space-time discontinuous Galerkin schemes for hyperbolic systems of conservation laws
Abstract:
We propose and analyse a space-time discontinuous Galerkin (DG) finite element method for hyperbolic systems of conservation laws. To ensure entropy stability, the discretisation is performed in entropy variables and entropy-stable numerical fluxes are used. As solutions of hyperbolic conservation laws can develop discontinuities (shocks) in finite time, we include a streamline diffusion and a shock-capturing term in the formulation to suppress spurious oscillations in the vicinity of shocks. The approximate solutions are shown to converge to an entropy measure-valued solution for systems of conservation laws.
We have considered a large number of problems for instance for Burgers' equation, the wave equation, and the Euler equations in one or two spatial dimensions. These experiments demonstrate the robustness and the high-resolution properties of the scheme.
Christian Klingenberg (Würzburg University)
Title : Examples of mathematical modeling - are they a paradigm for modeling biological phenomena?
Abstract :
This talk is geared towards a general audience. I will discuss natural phenomena that are described by physical rules and thus lend themselves to a mathematical description. These are typically in the form of differential equations that need to be studied using mathematical analysis and solved approximately using numerical methods. This shall be illustrated with examples where this is successful. We then raise the question if this could be applied to biological phenomena.
Jens Klotzky (Würzburg University)
Title : Admissibility conditions for discontinuous flux conservation laws
Abstract :
A discontinuity in space of the flux of a conservation law results in a jump that requires its own admissibility condition. This is given by the germ-condition described in the paper by Adrianov, Karlsen and Risebro (2011). This germ admissibility condition requires the knowledge of a trace at this jump. In this talk we report on progress in formulating the germ admissibility condition without needing traces. We use the kinetic formulation for this. This is joint work with Christian Klingenberg and Nicolas Seguin.
Ujjwal Koley (Tata Institute, Bangalore, India)
Title : Convergence of Higher order Schemes for Korteweg de-Vries (KdV) equation.
Abstract :
We consider the KdV equation used for modeling, e.g., water waves in a narrow channel. The time evolution is described by a quadratic (Burgers') plus a linear (Airy) term.The aim of this talk is to show convergence of higher order schemes with less regular initial data. Finally, the convergence is illustrated by several examples.
Sudarshan Kumar (Conception, Chile)
Title: On numerical methods for two-phase flow in porous media
Abstract:
Two phase flow in porous media is well known for its high importance in many of the industrial and engineering applications like petroleum reservoir, sedimentation process, water management in polymer electrolyte
fuel cells, environmental remediation etc. By the two phase flow we mean the simultaneous flow of two fluids ( for instance oil and water) and a porous medium is a substance that contains pores, or spaces between solid material through which liquid or gas can pass. Examples of naturally occurring porous media include sand, soil, some types of stone, human lungs etc. This flow process is modeled by a set of partial differential equations of which the exact solution could be used to describe the flow process or to predict the behavior of the flow in advance. Unfortunately for several reasons its hard to obtain such solutions, however on the other hand the entire industry increasingly relies on the numerical simulation of the model equations. Apparently the complexities in the flow process make it hard to conduct an accurate numerical simulation of the underlying physical model. In this talk we discuss about these issues and introduce a numerical method which resolves these difficulties up to a certain extend. Also we present several numerical results to show the robustness of the proposed numerical scheme supplemented with its mathematical analysis.
Sibusiso Mabuza (Würzburg University)
Title : Mathematical modeling and simulations of drug carriers in blood vessels.
Abstract :
We In this talk, we introduce some mathematical models for studying the flow of blood and blood solutes in the human cardiovascular system. We start by discussing the constitutive laws for simplified blood flow and reactive chemical solute transport in two dimensions. What we get is systems of coupled nonlinear differential equations. We then discuss the numerical solution techniques used to solve these equations and present some numerical simulations in simplified cases. Lastly, we discuss the future direction of the work.
Hélène Mathis (Nantes University, France)
Title : Modeling phase transition and metastable phases
Abstract :
We are interested in the modeling of liquid-vapor phase change which are of major importance in several industrial applications. The phenomena we are interested in are complex phase changes including the appearance of metastable states.
Metastable vapor is a gaseous state where the pressure is higher than the saturation pressure. Such states are very unstable and a very small perturbation brings out a droplet of liquid inside the gas.
In the first part of the talk, we explain the thermodynamics of two-phase fluid. Then we introduce a dynamical system that is able to depict the mass transfer between the two phases, for which equilibrium states are either metastable states, stable states or mixture states.
Jirı Neustupa (Czech Academy of Sciences, Prague, Czech Republic):
Title: On the problem of regularity of weak solutions to the Navier–Stokes equations
Abstract: The Navier–Stokes equations for the viscous incompressible fluid have been known and used already for about two hundred years. The question of regularity of weak solutions to these equations is so important and challenging that it was named among the seven so called “millenium problems” by the Clay Institute of Mathematics. We know from the pioneering works of J. Leray and E. Hopf in the first half of the 20th century that the Navier–Stokes equations have a weak solution on a time interval of an arbitrary length. However, in spite of a great effort of several generations of specialists in PDE’s, the question whether a singular point (where the so called “blow up” occurs) can develop in the existing weak solution, remains open. One of the reasons why the question goes beyond the scope of the pure mathematics is its close relation to the question of uniqueness. We explain the nature of the problem and give a brief survey of important partial results in this field, including some recent contributions.
Marica Pelanti (ParisTech, Paris)
Title: A preconditioned scheme for a two-phase compressible flow model at low Mach number
Abstract: We describe two-phase compressible flows by a hyperbolic single-velocity two-phase flow model with stiff mechanical relaxation. In particular, we are interested in the simulation of liquid-gas mixtures such as cavitating flows, which are relevant in numerous engineering devices. The model equations are numerically approximated via a fractional step algorithm, which alternates between the solution of the homogeneous hyperbolic portion of the system through wave propagation finite volume schemes, and the solution of a system of ordinary differential equations that takes into account the pressure relaxation terms. When used in this algorithm, classical schemes such as Roe's or HLLC prove to be very efficient to simulate the dynamics of transonic and supersonic flows. Unfortunately, these methods suffer from the well known difficulties of loss of accuracy and efficiency for low Mach number regimes encountered by upwind finite volume discretizations. This issue is particularly critical for liquid-gas flows due to the large and rapid variation of the Mach number, since the speed of sound may range from very low values in the two-phase mixture to very large values in the liquid medium. To cure the problem of loss of accuracy at low Mach number, in this work we extend to the considered two-phase flow model the strategy of the preconditioned Roe-Turkel scheme of Guillard--Viozat [Computers & Fluids, 28, 1999] for the single-phase Euler's equations. A suitable set of entropic variables for the two-phase system is chosen to define the Turkel-type preconditioning matrix that corrects the numerical dissipation term of the finite volume scheme at low Mach number.As for the single-phase case, the resulting technique alters only the acoustic characteristic fields of the model at low Mach number, while interface (contact) waves are preserved unchanged. We present numerical results for two-dimensional liquid-gas channel flow tests that show the effectiveness of the proposed preconditioned method for the two-phase system. In particular, we show that in the low Mach number limit pressure perturbations at the discrete level correctly scale with the square of the reference Mach number, in agreement with the theoretical results for the continuous two-phase flow model.
Marlies Pirner (Würzburg University)
Title: On a kinetic multi species BGK model
Abstract: We shall begin by introducing the kinetic description of a fluid flow, make some simplifying assumption, and arrive at the the so called BGK kinetic equation, which is an equation of Boltzmann type. We then describe a two species version of such a BGK model that has all the desired properties one needs from such a model. We finish by describing the connection between this model and fluid models for plasma, including inviscid and viscous models. This is joint work with Gabriella Puppo und Christian Klingenberg.
Johanna Ridder (Oslo, Norway)
Title: A convergent finite difference scheme for the Ostrovsky-Hunter equation
Abstract:
The Ostrovsky-Hunter equation describes small-amplitude shallow water waves in a rotating fluid. We propose a finite difference scheme for this equation with periodic boundary conditions and show that the solution of the scheme satisfies discrete energy estimates. These estimates allow us to use Tartar's compensated compactness and prove convergence to a weak solution. Numerical experiments confirm the convergence.
Tobias Ramming (Bayreuth, Germany)
Title: A kernel-based discretisation method for first order partial differential equations of evolution type
Abstract:
We derive a new discretisation method for first order PDEs, which is based upon a meshfree spatial approximation. This spatial approximation is similar to the sph (smoothed particle hydrodynamics) technique and is a typical kernel based method. It differs, however, significantly from the sph method since it employs an Eulerian and not a Lagrangian approach. We prove stability and convergence for the resulting semi-discrete system under very mild assumptions on the right-hand side of the PDE. The approximation order depends on the underlying kernel and the smoothness of the solution.
Giuseppe Straquidanio (Catania, Italy)
Title: On numerical methods for equations of BGK type.
Abstract:
In hydrodynamic regimes, fluid flows can be described by standard models such as Navier-Stokes or compressible Euler equations. However, some regimes cannot be qualified as hydrodynamic and the continuum equations are not able to correctly describe the dynamics of the flow. When the regime is qualified as rare fied (large Knudsen number) it is well described by the Boltzmann equation.The mathematical difficulties related to the Boltzmann equation make it extremely difficult to treat; in particular, analytical solutions in most relevant situations are hard (and sometimes impossible) to find. Most of the difficulties are due to the multidimensional structure of the collision integral.For such reasons many numerical methods have been developed in the last decades. The most famous examples are Direct Simulation Monte Carlo, which is aparticle solver especially efficient in the rare fied regime. However, the computational time requirement increases very rapidly as the hydrodynamic regime is reached. A reduction of computation time is possible by considering simpli fied models of the Boltzmann. A particularly successful model is the BGK model, in which the collisionterm of the Boltzmann equation is replaced by a relaxation term, simpler to treat. In this lecture I will introduce the numerical methods for BGK model developed recently and the results obtained by me during my PhD.
References:
[1] G. Stracquadanio, "High order semi-Lagrangian methods for BGK-type models in the kinetic theory of rare ed gases", Ph.D. thesis, University of Parma, Italy, Jan. 2014.
[2] M. Groppi, G.Russo, G.Stracquadanio, "High order semilagrangian methods for BGK models". Preprint n.519, Department of Mathematics and Computer Science, University of Parma, 2014, accepted for publication in COMMUN MATH SCI, to appear.
Rony Touma (Beirut, Lebanon)
Title: Well-balanced central schemes for shallow water equations with wet and dry states
Abstract: In this talk we discuss a new well-balanced unstaggered central finite volume scheme for the shallow water equations on variable bottom topographies, with wet and dry states. Based on a special piecewise linear reconstruction of the cell- centered numerical solution and a careful discretization of the system of partial differential equations, the proposed numerical scheme ensures both a well- balanced discretization and the positivity requirement of the water height component. More precisely the well-balanced requirement is fulfilled by following the surface gradient method while, the positivity requirement of the computed water height component is ensured by following a new technique specially designed for the unstaggered central schemes. Numerical experiments are presented at the end of the talk.
Feng Xie (Shanghai, China)
Title: Local existence of solutions to the Prandtl equations from compressible flow in two space dimensions.
Abstract: As we all know that the boundary layer phenomena is a very important topic in fluid dynamics, kinetic theory and so on. In this talk we shall review some results for the classical Prandtl equations for incompressible flow. As a natural extension, we shall derive the related boundary layer equations by multi-scale expansion method, and then consider the local existence of solutions to these boundary layer equations in some suitable Sobolev spaces.