Research Areas
Inverse problems are problems where one wants to draw conclusions about a hidden cause from an observable effect. This leads to a variety of connections within mathematics, but also to interdisciplinary applications in biophysics and the life sciences. The main research topics in our group are:
Statistical inverse problems and regularization theory:
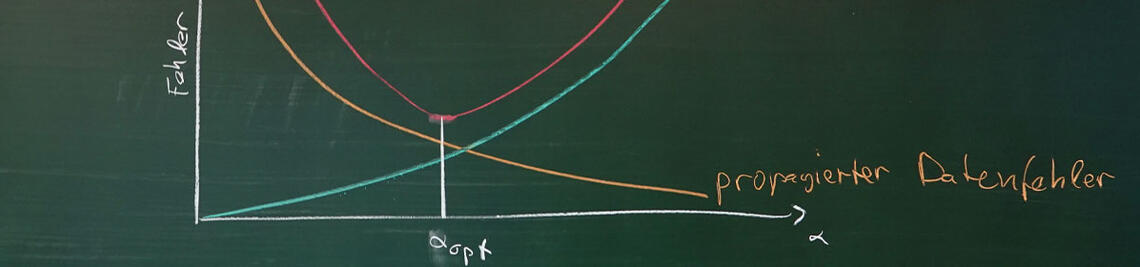
To solve an inverse problem, so-called regularization methods are used, which are adapted to the structure of the problem on the one hand and to the nature of the observations, i.e. especially to the unavoidable noise, on the other hand. We develop and investigate such procedures, and characterize in particular the influence of the noise modeled as random on the reconstructions. This requires a combination of different techniques from functional analysis and probability theory.
Quantification of uncertainties using multiple hypothesis testing:
In addition to obtaining suitable reconstructions, qualitative statements ("inference") about the unknown cause are also of interest. Here we pursue the goal of obtaining local statements, e.g. about homogeneity or monotony by means of statistical hypothesis testing. Again, techniques from different areas of mathematics are helpful.
Applications in the experimental sciences:
In addition to the theoretical analysis of regularization and inference methods, the numerical implementation of the same as well as the application in interdisciplinary cooperation are of interest. One of our research focuses in this area is high-resolution fluorescence microscopy, where methods developed by us allow conclusions to be drawn about the location and number of molecules existing in a sample.