Wegweiser MΦ
Im Studiengang Mathematische Physik haben Sie sowohl im Bachelor als auch im Master eine große Freiheit, Vorlesungen zu wählen. Um hier eine sinnvolle Auswahl und vor allem eine gute Reihenfolge zu gewährleisten, braucht es eine gewisse Übersicht, nicht zuletzt auch, um zum richtigen Zeitpunkt die passenden Grundlagen für die Physikvorlesungen zu erhalten.
Bachelorstudium
Die nachfolgende Liste gibt eine Auswahl an Vorlesungen im Bachelorstudium mit ihren wechselseitigen Verbindungen und insbesondere ihren Beziehungen zu Vorlesungen im Physikteil des Bachelorstudiums in der mathematischen Physik. Die Einschätzungen sollten weitgehend als aus der Sicht von Lehrstuhl X geschrieben verstanden werden, mögen aber vielleicht trotzdem bei der Auswahl einer Reihenfolge nützlich sein. Insbesondere bei Interesse an einer Bachelorarbeit am Lehrstuhl X sind die folgenden Vorlesungen sehr hilfreich.
Die Vorlesung Elementare Differentialgeometrie behandelt die Geometrie von Kurven und Flächen im (drei-dimensionalen) Euklidischen Raum. Hier wird als wesentliche Eigenschaft der Kurven und Flächen deren Krümmung studiert. Damit kann man diese Vorlesung als Vorgriff auf eine Riemannsche Geometrie im Master sehen. Für diesen einfachsten Fall von Flächen lassen sich dann aber auch erste tiefe Sätze zum Verhältnis lokaler Information wie der Krümmung zu globalen Eigenschaften der Fläche wie etwa ihre Euler-Zahl finden.

Das Studium der Kurven und Flächen bezieht seinen großen Charme vor allem daraus, dass die Problemstellungen wie auch die Resultate sehr anschaulich visualisiert werden können, nicht zuletzt mit Hilfe sehr leistungsfähiger Computerprogramme. Auf einer konzeptuelleren Ebene lernt man in dieser Vorlesung auch die an vielen anderen Stellen in der Mathematik nützliche Fähigkeit, dem geometrischen Problem angepasste Koordinaten zu finden. Anschließende Rechnungen sind zwar immer sehr explizit und erfordern selten mehr als den üblichen Kalkül der Vektoranalysis, können aber durch geschickte Koordinaten erheblich vereinfacht und abgekürzt werden.
Für die mathematische Physik ist das Studium von Kurven und Flächen vor allem deshalb sehr nützlich, um die Parametrisierungen verschiedenster geometrischer Objekte durch angepasste Koordinaten zu verstehen. Diese Einsichten können dann in verschiedenen weiterführenden Vorlesungen gewinnbringend eingesetzt werden, wenn die Flächen beispielsweise die Randbedingungen einer partiellen Differentialgleichung beheimaten oder Zwangskräfte die Bewegungen eines Teilchen auf die Fläche einschränken. Somit finden sich schnell Anwendungen in der Feldtheorie sowie der Lagrangeschen oder Hamiltonschen Mechanik.
Die Funktionalanalysis behandelt analytische Fragestellungen in unendlichen Dimensionen. Hier sind insbesondere die Analysis mit Banach- und Hilbert-Räumen zu nennen, aber auch weitere und kompliziertere Situationen wie lokal-konvexe Räume werden betrachtet.
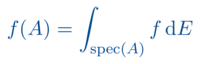
In der mathematischen Physik sind Techniken und Resultate der Funktionalanalysis an vielen Stellen erforderlich: in der klassischen Feldtheorie wie etwa der Elektrodynamik, aber auch in der Strömungsmechanik oder Kontinuumsmechanik werden diejenigen Aspekte der Funktionalanalysis gebraucht, welche zu Ergebnissen in der Theorie der partiellen Differentialgleichungen führen, um dann eben das Lösungsverhalten der Feldgleichungen zu studieren. Der aber vielleicht fundamentalere Gebrauch von Funktionalanalysis findet in der Quantentheorie statt: diese beiden Gebiete wurden nicht zuletzt parallel zu Beginn des 20. Jahrhunderts größtenteils von denselben Personen entwickelt, eine Zeit in der die wechselseitige Inspiration von Mathematik und Physik besonders groß und fruchtbar war. Insbesondere die Spektraltheorie ist nach wie vor für beide Gebiete von zentraler Bedeutung und verfolgt auch die gleichen Ziele: Spektren von selbstadjungierten Operatoren auf Hilbert-Räumen zu verstehen ist sowohl in der Quantentheorie als auch in der Funktionalanalysis eine zentrale Problemstellung.
Am Lehrstuhl X benötigen wir funktionalanalytische Themen vor allem im Hinblick auf ein tiefergehendes Verständnis von quantenmechanischen Observablenalgebren. Hierfür ist die Bachelorvorlesung zur Funktionalanalysis das unumstrittene Fundament. Auch für weiterführende Veranstaltungen in der mathematischen Physik wie etwa der Mastervorlesung Algebra und Dynamik von Quantensystemen wird am Lehrstuhl X eifrig Gebrauch von funktionalanalytischen Techniken gemacht.

Auf der konzeptuellen Ebene geht es vor allem darum, Konvergenz und Vollständigkeit solcher Räume sowie die Stetigkeitseigenschaften linearer Abbildungen zwischen derartigen Räumen zu verstehen. Ein großes Themengebiet ist dann die Spektraltheorie, wo versucht wird, die einfache Situation der linearen Algebra in endlichen Dimensionen auch auf diese allgemeineren Vektorräume zu übertragen. Rein algebraisch ist dies nicht weiter sinnvoll, es müssen eben nun viele analytische Resultate zu Hilfe genommen werden, um Spektren definieren zu können und angemessene Analoga von Diagonalisierbarkeit zu formulieren.
Konkret werden spezielle Funktionenräume wie etwa glatte, stetige oder auch nur integrable Funktionen betrachtet. Diese erweisen sich bezüglich der richtigen Normen dann als Banach- oder Hilbert-Räume, in manchen Fällen benötigt man hier auch allgemeine lokal-konvexe Räume. Fragen nach der Vollständigkeit und den topologischen Dualräumen sind in diesen konkreten Beispielen von fundamentaler Bedeutung und erfordern typischerweise bereits erheblichen Aufwand. Das Studium von Operatoren auf solchen Funktionenräumen wie etwa Differentialoperatoren führt dann schnell zu Anwendungen in der Theorie der partiellen Differentialgleichungen.
In der Funktionentheorie studiert man Funktionen auf offenen Teilmengen der komplexen Ebene und ihre Holomorphie, also ihre komplexe Differenzierbarkeit. Hier zeigt sich, dass viele Komplikationen aus der reellen Analysis auf wunderbare Weise vereinfacht werden. Der inneren Ästhetik der Funktionentheorie kann man sich schwer entziehen, womit dieser Teil der Mathematik unbedingt zur Allgemeinbildung in einem jeden Bachelorstudium der Mathematik gehört.
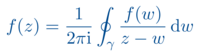
Für die mathematische Physik ist die Funktionentheorie eher mittelbar von Bedeutung, dann aber durchaus auf sehr vielfältige Weise: zum einen werden viele wichtige transzendente Funktionen in der Mathematik mit Techniken der Funktionentheorie definiert und studiert. Solche Funktionen treten oft als spezielle Lösungen von Differentialgleichungen in der mathematischen Physik auf, wie etwa die Bessel-Funktionen. Zum anderen liefert die Funktionentheorie neue Methoden, verschiedenste Integrale auf zum Teil überraschend einfache Weise zu berechnen, und erweist sich damit als ein sehr leistungsfähiges Werkzeug.
Eher konzeptuell sind nun die Anwendungen der Funktionentheorie beispielsweise in der Quantenfeldtheorie, wo die holomorphe Fortsetzung gewisser Funktionen (und Distributionen), wie etwa der verschiedenen Mehrpunktfunktionen, aus denen dann entscheidende Aussagen über die Quantenfeldtheorie getroffen werden können. Prominente Beispiele solcher Resultate sind das CPT-Theorem und das Spin-Statistik-Theorem. Auch bei der Betrachtung von Operatoralgebren oder allgemeinerer Banach-Algebren liefert die Funktionentheorie wichtige Hilfsmittel. So wird beispielsweise in der Vorlesung Algebra und Dynamik von Quantensystemen ein holomorpher Kalkül entwickelt werden, der es erlaubt, holomorphe Funktionen eines Algebraelements in sinnvoller Weise zu definieren. Schließlich gibt es eine große Welt der komplexen Mannigfaltigkeiten, welche analog zur Differentialgeometrie der reellen Mannigfaltigkeiten aufgebaut werden kann, aber ihre eigenen Methoden und Resultate liefert. Hier finden sich weitere vielfältige Anwendungen in der mathematischen Physik, etwa der Kähler-Geometrie in der Geometrischen Mechanik.
Am Lehrstuhl X verwenden wir funktionentheoretische Techniken zum einen in der Kähler-Geometrie als Teilgebiet der symplektischen Geometrie. Hier können bestimmte Quantisierungsverfahren auf besonders einfache Weise durchgeführt werden, wobei die Funktionentheorie eine große Rolle spielt. Aber auch beim Studium allgemeiner Observablenalgebren spielt die Existenz eines holomorphen Kalküls immer eine große Rolle.
In der Bachelorvorlesung Geometrische Analysis werden die analytischen Konzepte der Analysis-Grundvorlesungen weiterentwickelt. Das große Ziel ist der (allgemeine) Satz von Stokes für Untermannigfaltigkeiten des Euklidischen Raums. Daraus erhält man dann eine Vielzahl von bekannten Integralsätzen, wie den Satz von Gauss, den Satz für Stokes, die Greensche Integralformel etc.
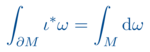
Um dieses Ziel zu erreichen, werden zunächst Untermannigfaltigkeit, also die höher-dimensionalen Analoga von parametrisierten Flächen, diskutiert. Hierfür muss dann in einem zweiten Schritt der Kalkül von Differentialformen etabliert werden, für welche dann eine Integrationstheorie entwickelt wird. Der Satz von Stokes ist dann letztlich nur eine mehr-dimensionale Verallgemeinerung des Hauptsatzes der Differential- und Integralrechnung.
Die Bedeutung der Integralsätze in der mathematischen Physik ist kaum zu überschätzen: insbesondere in Feldtheorien wie etwa der Elektrodynamik lassen sich Teile der Feldgleichungen so verstehen, dass zum einen die Felder durch Differentialformen beschrieben werden, und zum anderen die Differentialformen geschlossen sind, also ihre Integrale über geeignete Untermannigfaltigkeiten verschwinden. Damit werden der Satz von Stokes und seine Varianten unmittelbar Gegenstand der klassischen Feldtheorie. Aber auch zuvor finden die Integralsätze und der Kalkül mit Differentialformen vielfältige Anwendungen in der mathematischen Physik, beispielsweise in der Hamiltonschen Mechanik und der Thermodynamik. Die Begriffe der Differentialformen und Untermannigfaltigkeiten werden später in der Differentialgeometrie in einen konzeptuell klareren Zusammenhang gestellt.
Für die Arbeit am Lehrstuhl X bedeutet die geometrische Analysis eine Vorstufe zur Differentialgeometrie, welche dann im Master eines der zentralen Themengebiete sein wird. Daher ist diese Vorlesung als Vorbereitung und Einstimmung auf die zentralen Themen am Lehrstuhl X zu verstehen, auch wenn es eine gewisse thematische Überschneidung mit der Masterveranstaltung zur Differentialgeometrie gibt.
Gewöhnliche Differentialgleichungen treten an vielen Stellen in der Mathematik und der mathematischen Physik auf: grob gesprochen kann man eine gewöhnliche Differentialgleichung immer als eine Gleichung zur Zeitentwicklung verstehen.
Die ersten wichtigen Fragen zu gewöhnlichen Differentialgleichungen sind, wie immer in der Mathematik, die Fragen nach der Lösungstheorie derartiger Gleichungen. Hier interessiert man sich insbesondere für die Existenz und Eindeutigkeit von Lösungen bei gegebenen Anfangsdaten. Aber auch Randwertprobleme, wo die Lösungen zu einem Anfangs- und Endzeitpunkt vorgegeben werden, sind von großem Interesse.

Neben den konzeptuellen Fragen werden in der Vorlesung zu gewöhnlichen Differentialgleichungen auch konkrete Beispiele und Beispielklassen betrachtet, für die eine explizite Lösung gefunden werden soll. Hier ist insbesondere die Klasse der linearen Differentialgleichungen von Interesse, da die Lösungen hier einen Vektorraum bilden. Zudem können durch Differentialgleichungen wichtige transzendente Funktionen definiert werden: hier sind beispielsweise die Bessel-Funktionen zu nennen, die als Lösungen der Besselschen Differentialgleichung auftreten. Viele der wichtigen speziellen Funktionen erhält man auf diese Weise.
In der mathematischen Physik treten gewöhnliche Differentialgleichungen letztlich in allen Bereichen auf. Vornehmlich ist hier die Mechanik zu nennen, wo die Newtonschen Bewegungsgleichungen als eine gewöhnliche Differentialgleichung zweiter Ordnung für die Kurve eines Teilchens gesehen werden kann. Dies führt dann auch auf eine speziellere Klasse von gewöhnlichen Differentialgleichungen, nämlich die Hamiltonschen Gleichungen. Hier ist, anders als im allgemeinen Fall, immer eine Erhaltungsgröße gegeben, die Energie des Systems. Aber auch ohne Energieerhaltung sind Differentialgleichungen in der mathematischen Physik von großem Interesse: wann immer man Systeme mit Reibung betrachtet, benötigt man dazu dissipative Differentialgleichungen.
Schließlich liefern die gewöhnlichen Differentialgleichungen auch oftmals wichtige Techniken und Resultate, die in weiterführenden Veranstaltungen wie etwa der Differentialgeometrie oder den partiellen Differentialgleichungen benötigt werden.
Am Lehrstuhl X werden gewöhnliche Differentialgleichungen vor allem im Zusammenhang mit Anwendungen in der Differentialgeometrie benötigt, insbesondere um die Lösungstheorie der Hamiltonschen Gleichungen in der Geometrischen Mechanik zu verstehen.
Partielle Differentialgleichungen sind Gleichungen für Funktionen mehrerer Variablen, welche Bedingungen an die Ableitungen der gesuchten Funktion stellen. Eine wesentliche Interpretation von partiellen Differentialgleichungen ist, dass es sich um Feldgleichungen handelt, die gesuchte Funktion kann als Feld auf einer Raumzeit oder nur auf dem Raum gesehen werden.
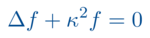
Neben den üblichen Fragen nach der Existenz und Eindeutigkeit von Lösungen wird es je nach Typ der partiellen Differentialgleichung wichtig, Anfangswertprobleme (Cauchy-Probleme) oder Randwertprobleme zu studieren. Anfangswertprobleme legen die Lösung auf einer Cauchy-Fläche fest und suchen nach einer Zeitentwicklung der Anfangsdaten in der ganzen Raumzeit. Eine wichtige Frage ist hier dann die stetige Abhängigkeit der Lösung von den Anfangsdaten und eventuell von weiteren Parametern. Randwertprobleme fixieren die Lösung auf dem geometrisch mitunter recht komplizierten Rand eines Gebietes und suchen nach einer Lösung in dessen Innerem. Zudem können beide Aspekte kombiniert werden.

Konkrete Beispiele von partiellen Differentialgleichungen erhält man beispielsweise aus den Feldgleichungen der Elektrodynamik, also den Maxwell-Gleichungen, aber auch die Einsteinschen Feldgleichungen der allgemeinen Relativitätstheorie sind partielle Differentialgleichungen, nun sogar auf einer differenzierbaren Mannigfaltigkeit. Verschiedene relativistische Feldgleichungen sind dann der klassische Ausgangspunkt für Quantenfeldtheorien, für deren Formulierung immer ein gutes Verständnis der klassischen Gleichungen erforderlich ist. In diesem Umfeld sind auch die klassischen Yang-Mills-Gleichungen zu nennen. Aber auch die Bewegungsgleichungen von Flüssigkeiten, etwa die Euler-Gleichung oder die Navier-Stokes-Gleichung, sind partielle Differentialgleichungen, für die man das Anfangswertproblem verstehen will. Weitere Beispiele erhält man aus der Thermodynamik, wo die Wärmeleitungsgleichung eine partielle Differentialgleichung ist, die den Ausgleichsprozess bei unterschiedlichen Temperaturen beschreibt. Schließlich sind die Maxwell-Gleichungen der Elektrostatik bei Anwesenheit von Leitern typische Beispiele für Randwertprobleme.
Partielle Differentialgleichungen treten aber auch in der reinen Mathematik an verschiedensten Stellen auf. Hier ist beispielsweise die Differentialgeometrie zu nennen, wo die Wärmeleitungsgleichung auf einer Riemannschen Mannigfaltigkeit einen zentralen Baustein bei verschiedenen Index-Theoremen darstellt.
Am Lehrstuhl X werden partielle Differentialgleichungen als Feldgleichungen verstanden und dienen hier als der klassische Ausgangspunkt für Quantisierungsverfahren, welche typischerweise auf der Konstruktion von Greenschen Funktionen basieren. Insbesondere Wellengleichungen auf global-hyperbolischen Raumzeiten erweisen sich hierbei als eine reichhaltige und zugängliche Beispielklassen.
Die Topologie abstrahiert die Begriffe der offenen Teilmenge, der Stetigkeit und der Konvergenz von der aus den Grundvorlesungen bekannten Situation metrischer Räume hin zu allgemeinen topologischen Räumen. Damit ist die Topologie zum einen ein recht abstraktes Thema in der reinen Mathematik, zum anderen aber die unabdingbare Grundlage für viele weiterführende Veranstaltungen.

Der Begriff des topologischen Raumes erlaubt nun eine sehr allgemeine Formulierung von analytischen Fragestellungen wie etwa Stetigkeit, Konvergenz, Dichtheit und Nachbarschaften, aber auch sehr geometrische Fragestellungen wie Kompaktheit, Zusammenhang und Trennungseigenschaften. Damit wird die Topologie zum Ideengeber und Lieferant der weiterführenden Vorlesungen zur Funktionalanalysis aber auch der Differentialgeometrie.
Für die mathematische Physik kommt die Topologie zwar nur mittelbar zur Anwendung, vor allem eben über die Funktionalanalysis und die Differentialgeometrie.Letztlich bleibt aber ein Studium der mathematischen Physik ohne Kenntnisse der Topologie unvollständig: gerade in den an das Bachelorstudium anschließenden Veranstaltungen im Masterprogramm werden oft topologische Grundbegriffe verwendet, ohne die Zeit für eine detaillierte Einführung dafür zu haben. Im Lehrstuhl X sind dies vor allem die weiterführenden Veranstaltungen zur Funktionalanalysis im Bachelor und zur Differentialgeometrie im Master.
Masterstudium
Im Masterstudium der mathematischen Physik gibt es neben den beiden Pflichtvorlesungen eine Vielzahl von möglichen Kursen, die besucht werden können. Die folgende kommentierte Liste stellt nun einige der für eine Masterarbeit am Lehrstuhl X interessanten Veranstaltungen zusammen und zeigt wechselseitige Beziehungen untereinander sowie Anwendungen in den Physikvorlesungen auf.Zusätzlich zu den Vorlesungen sind selbstverständlich verschiedene Arbeitsgemeinschaften von Interesse. Hier bietet der Lehrstuhl X regelmäßig eine reichhaltige Auswahl an. Bei Interesse an einer Masterarbeit am Lehrstuhl X sollte eine sinnvolle Auswahl der folgenden Vorlesungen besucht worden sein. Darüber hinaus wird eine regelmäßige Teilnahme am Seminar Deformationsquantisierung erwartet.
Die Vorlesung Algebra und Dynamik von Quantensystemen im Master ist eine der beiden Pflichtveranstaltungen. Auf physikalischer Seite steht hier die Quantentheorie im Vordergrund, wobei der Fokus auf konzeptuellen Fragen ist: die Struktur einer Quantentheorie wird durch ihre Observablenalgebra bestimmt, Zustände sind ein daraus abgeleitetes Konzept und Darstellungen der abstrakten Observablenalgebra durch konkrete Operatoren müssen im Detail studiert werden.
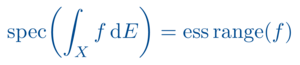
Die mathematischen Techniken der Theorie der C*-Algebren und der Operatoralgebren werden vor allem in axiomatischen Zugängen zur Quantentheorie und dort vor allem in der axiomatischen Quantenfeldtheorie (AQFT) benutzt. Hier bieten die Haag-Kastler Axiome einen sehr allgemeinen Rahmen dafür, was eine Quantenfeldtheorie auf dem Minkowski-Raum sein soll. Diese Sichtweise wurde insbesondere in den letzten Jahren stark erweitert und auf beliebige global-hyperbolische Raumzeiten ausgedehnt.
Am Lehrstuhl X werden die algebraischen Aspekte einer Observablenalgebra eingehend studiert. Ein wichtiger Aspekt ist hierbei die Konstruktion einer quantenmechanischen Observablenalgebra ausgehend von klassischen Daten. Hier verwenden wir vor allem die Technik der Deformation von Algebren. Dabei stellen sich im Anschluss an die algebraischen Fragen vor allem Fragen funktionalanalytischer Natur, da die Algebren typischerweise nicht oder zumindest nicht auf einfache Weise C*-Algebren sind. Deshalb werden auch andere Arten von topologischen Algebren betrachtet.

Observablen in der Quantenphysik werden durch eine nichtkommutative *-Algebra beschrieben. Bereits auf rein algebraischer Seite können dann Zustände als positive Funktionale sowie Darstellungen auf Prä-Hilbert-Räumen beschrieben werden. Um jedoch physikalisch brauchbare Spektren und Spektralmaße definieren zu können, ist ein nicht unerheblicher analytischer Aufwand von Nöten. Hier gibt es verschiedene analytische Anforderungen an die Observablenalgebra, die in der Definition einer C*-Algebra gipfeln. Für diese kann dann ein brauchbarer Spektrumsbegriff etabliert werden, welcher mit einem stetigen Kalkül einhergeht. Um Darstellungen zu verstehen, sind dann im Anschluss ein genaueres Studium der Operatoren auf einem Hilbert-Raum sowie eine Erweiterung des stetigen Kalküls zu einem messbaren Kalkül erforderlich. Unbeschränkte Operatoren auf einem Hilbert-Raum bilden schließlich den Ausgangspunkt, um in der Quantentheorie über die Schrödinger-Gleichung eine Dynamik zu definieren. Hier ist der Begriff der Selbstadjungiertheit von entscheidender Bedeutung.
Die Vorlesung kann in gewisser Hinsicht als eine Fortführung der Funktionalanalysis aus dem Bachelorstudium gesehen werden. Die dort erzielten Ergebnisse zu Banach- und Hilbert-Räumen werden hier weiter benutzt und verfeinert, was insbesondere das Studium der Operatoren auf solchen Räumen einschließt. Es kommen aber durchaus auch Techniken der Funktionentheorie und der mengentheoretischen Topologie zum Einsatz.
Die Vorlesung Analysis und Geometrie klassischer Systeme ist die zweite Pflichtveranstaltung im Masterstudium Mathematische Physik. Hier werden, durchaus mit größeren Variationen von Jahr zu Jahr, analytische sowie geometrische Aspekte von Systemen der klassischen Physik betrachtet. Ein wichtiges zentrales Thema sind dabei die klassischen Feldtheorien, für die zum einen geometrische Techniken entwickelt werden, um Formulierungen zu erhalten, die auf allgemeinen Raumzeiten Gültigkeit haben. Zum anderen müssen ausgefeilte analytische Methoden aufgeboten werden, um die Lösungstheorien der Feldgleichungen, welche typischerweise partielle Differentialgleichungen sind, zu verstehen.
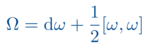
Als Feldtheorien werden hier zum einen Systeme der Kontinuumsmechanik und Strömungsmechanik betrachtet, wo die Feldgleichungen die Bewegungen und Deformationen von Festkörpern oder aber das Fließverhalten von Flüssigkeiten beschreiben. Die zweite Variante der Vorlesung betrachtet Feldgleichungen der Teilchenphysik, vor allem die klassischen Yang-Mills-Gleichungen, und stellt so die klassischen Ausgangspunkte der gängigen Quantenfeldtheorien in einen differentialgeometrischen Kontext. Auf mathematischer Seite wird dazu, aufbauend auf Resultaten zur Differentialgeometrie, die Theorie der Hauptfaserbündel und ihrer Zusammenhänge entwickelt. Hier steht zunächst die Geometrie sehr stark im Vordergrund. Analytische Fragestellungen zur Lösungstheorie erweisen sich anschließend als durchweg schwierig. Eine dritte Variante der Vorlesung betrachtet (lineare) Wellengleichungen auf allgemeinen Raumzeiten, also Pseudo-Riemannschen Mannigfaltigkeiten mit Lorentz-Signatur, wie sie in der Relativitätstheorie gebraucht werden. Hier kann bei genügend guten Voraussetzungen an die Raumzeit eine globale Lösungstheorie gefunden werden. Je nach Vorwissen werden Aspekte der Differentialgeometrie, der Lie-Gruppen, und der Raumzeiten aus der Lorentz-Geometrie kurz wiederholt.
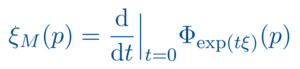
Am Lehrstuhl X werden die differentialgeometrischen Ergebnisse dieser Vorlesung auf vielfältige Weise benötigt und weitergeführt. Zum einen ist die Theorie der Hauptfaserbündel nicht nur Ausgangspunkt für Yang-Mills-Feldtheorien sondern auch die Basis für das Studium von Gruppenwirkungen von Lie-Gruppen ganz allgemein. Solche treten dann auch in vielen anderen Situationen wie beispielsweise in der Geometrischen Mechanik auf. Aber auch Aspekte der Wellengleichungen auf global-hyperbolischen Raumzeiten spielen bei uns eine zunehmend starke Rolle. Die Lösungstheorie mittels Green-Operatoren dient als Ausgangspunkt verschiedener Quantisierungsmethoden.
Die Mastervorlesung Differentialgeometrie ist eine Fortführung der Bachelorvorlesungen Geometrische Analysis und Elementare Differentialgeometrie. Hier stehen nun abstrakte Mannigfaltigkeiten im Zentrum der Betrachtung. Als sehr nützliches Vorwissen für diese Vorlesung kann man die mengentheoretische Topologie ansehen.

Differenzierbare Mannigfaltigkeiten werden als bestimmte topologische Räume mit zusätzlichen Eigenschaften, einer differenzierbaren Struktur, definiert, die es erlauben, intrinsisch (also ohne eine Einbettung als Teilmenge eines euklidischen Raums) von Differenzierbarkeit und Tangentialräumen zu sprechen. Dazu ist zunächst ein nicht unerheblicher begrifflicher Aufwand erforderlich. Dann allerdings erhält man eine sehr leistungsfähige Theorie um geometrische Fragen in koordinatenfreier Weise zu formulieren.

In der mathematischen Physik gibt es vielleicht zwei wirklich wichtige Strömungen, was die Verwendung moderner mathematischer Konzepte angeht: zum einen die funktionalanalytischen Techniken, die in jedweder Form von Quantentheorie von Nöten sind. Zum anderen findet eine Geometrisierung physikalischer Theorien auf fast jedem Gebiet statt. Hier ist die allgemeine Relativitätstheorie natürlich nur ein besonders prominentes Beispiel, aber auch die Yang-Mills-Theorien für die Wechselwirkungen in der Teilchenphysik ebenso wie die Frage nach Spinoren führen am Ende auf neue geometrische Formulierungen und Einsichten. Topologische Eigenschaften spielen zudem eine immer größere Rolle beispielsweise in der Festkörperphysik. Aus diesem Grund ist die Differentialgeometrie als eine der wichtigen Säulen einer jeder modernen physikalischen Theorie anzusehen und sollte von daher auch in keinem Studium der mathematischen Physik fehlen.
Am Lehrstuhl X ist eine grundlegende Kenntnis von Differentialgeometrie wohl nahezu unabdingbar. Selbst für die eher algebraischen oder funktionalanalytischen Fragestellungen am Lehrstuhl X bietet die Differentialgeometrie doch immer die entscheidenden Beispiele, die Motivation und nicht zuletzt auch die Intuition dafür, was eigentlich getan werden soll. Es sind dann insbesondere auch die weiterführenden Vorlesungen zur Geometrischen Mechanik oder zur Pseudo-Riemannschen und Riemannschen Geometrie aber auch die Analysis und Geometrie klassischer Systeme, die für die Arbeit am Lehrstuhl X von Bedeutung und Interesse sind. Schließlich bildet die Differentialgeometrie die Ausgangsbasis für verschiedenste Arbeitsgemeinschaften, Seminare und nicht zuletzt die Masterarbeiten am Lehrstuhl X.
Die Vorlesung Geometrische Mechanik beschäftigt sich mit der Frage, wie die Lagrangesche und vor allem die Hamiltonsche Mechanik in einer differentialgeometrischen Sprache formuliert werden können. Es zeigt sich, dass dies im Falle der Hamiltonschen Mechanik durch den Begriff der symplektischen Mannigfaltigkeit auf das beste gelingt. Verschiedenste Aussagen aus den Physikvorlesungen zur klassischen Mechanik können so in einem differentialgeometrischen Kontext betrachtet und meistens auf viel klarere und einfachere Weise bewiesen werden. Damit wird diese Vorlesung zu einer konsequenten Fortführung der entsprechenden Bachelorvorlesungen in der Physik zur klassischen Mechanik. Die Relevanz für die mathematische Physik sollte damit klar sein.

Neben diesen Aspekten gibt es aber auch starke innermathematische Gründe, sich mit der symplektischen Geometrie zu beschäftigen. Es gibt verschiedenste Anwendungen in der angewandten und reinen Mathematik, von besonders leistungsfähigen numerischen Verfahren in der Theorie der gewöhnlichen Differentialgleichungen wie den symplektischen Integratoren bis zu tiefen Anwendungen in der Darstellungstheorie von Lie-Algebren und Lie-Gruppen. Weiter bietet die Kähler-Geometrie eine Schnittstelle von symplektischer Geometrie zu anderen Bereichen der Geometrie wie etwa der Riemannschen Geometrie oder der komplexen Differentialgeometrie.
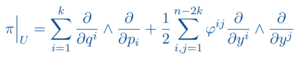
Stellt man die Poisson-Klammer der (geometrischen) Hamiltonschen Mechanik nun in den Vordergrund, so verallgemeinert sich die symplektische Geometrie zur Poisson-Geometrie: hier betrachtet man ganz allgemein Mannigfaltigkeiten mit einer Poisson-Klammer auf der Funktionenalgebra. Die Poisson-Geometrie ist nun ein besonders aktuelles und aktives Gebiet in der Differentialgeometrie, welches wiederum viele Anwendungen in der Physik erlaubt. Hier sind insbesondere Feldtheorien wie das Poisson-Sigma-Modell zu nennen. Aber auch in endlichen Dimensionen spielt die Poisson-Geometrie eine zentrale Rolle in verschiedensten Quantisierungstheorien.
Am Lehrstuhl X beschäftigen wir uns eingehend mit symplektischer Geometrie und Poisson-Geometrie. Auch wenn es sicherlich alternative Problemstellungen jenseits der symplektischen Geometrie bei uns gibt, ist es sicherlich so, dass alle Forschungsrichtungen auf mehr oder weniger direkte Weise Bezug zur symplektischen Geometrie besitzen. Aus diesem Grunde werden im Anschluss an die Vorlesung auch regelmäßig weiterführende Arbeitsgemeinschaften im Bereich der symplektischen Geometrie und der Poisson-Geometrie angeboten. Diese dienen dann nicht zuletzt aus Ausgangspunkt von Masterarbeiten.





