Guide for MΦ

In quantum physics, observables are described by a non-commutative *-algebra. Already on the purely algebraic side one can define states as positive functionals and describe representation on pre-Hilbert spaces. However, to obtain physically reasonable spectra and spectral measures one needs a non-trivial amount of analysis. Here several analytical requirements on the observable algebras can be asked, culminating in the definition of a C*-algebra. For  such algebras one has a useful notion of a spectrum in combination with a continuous calculus. To understand representations one needs a more detailed understanding of operators on a Hilbert space. Also  an extension of the continuous calculus to a measurable one is essential. Unbounded operators on a Hilbert space are then the starting point to define a dynamics in quantum theory by means of the Schrödinger equation. Here self-adjointness is of crucial importance.

This lecture can be seen as a particular continuation of Functional Analysis from the Bachelor program. The results from that lecture on Banach and Hilbert spaces are re-used and refined, including in particular the study of operators on such spaces. Moreover, some techniques from  Complex Analysis and Topology are needed.

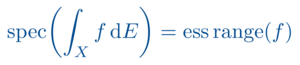
The mathematical techniques from the theory of C^*-algebras and operator algebras are used in axiomatic approaches to quantum theory and in particular in axiomatic quantum field theory (AQFT). Here the Haag-Kastler axioms provide a very general framework for the notion of quantum field theories on Minkowski space. In the recent years this point of view has been substantially refined and transferred to arbitrary globally hyperbolic spacetimes.

At Chair X the algebraic aspects of observable algebras are studied in detail. One important aspect is the actual construction of the quantum mechanical observable algebra starting from classical data. Here we use the techniques of deformation of algebras. In a second step questions about functional analytical properties of the algebras arise since the algebras are not or not directly C^*-algebras. For that reasons also other types of topological algebras are considered.

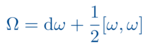
As field theories one can consider systems from continuum mechanics of fluid dynamics. There, the field equations describe the movements and deformations of solid state physics of the flow behavior of liquids, respectively. In the second variant of this course one considers field equations from particle physics, in particular the classical Yang-Mills  equations thus providing the classical starting point for the usual quantum field theories in a differential  geometric context. On the mathematical side, building on the results of Differential Geometry, the theory of principal fiber bundles and their connections need to be developed. There the main focus is on the geometry side of the story. Analytical questions on the solution theory prove to be highly non-trivial. A third version of the course considers (linear) wave equations on general spacetimes, i.e. on  Pseudo Riemannian Manifolds with Lorentz signature as they are needed in general relativity. For sufficiently nice spacetimes a global solution can be found. Depending on the pre-knowledge of the participants aspects of differential geometry, Lie groups and spacetimes are recalled at the beginning of the lecture.

Differentiable manifolds are defined as certain topological spaces with additional properties, a differentiable structure, which allow to speak intrinsically (i.e. without an embedding as a subset of a Euclidean space) of differentiability and tangent spaces. This initially requires a nontrivial conceptual effort. Once managed this hurdle one gets a very powerful theory to formulate geometric questions in a coordinate-free way.

In mathematical physics there are perhaps two really important trends concerning the use of modern mathematical concepts: on the one hand the functional-analytic techniques which are necessary in any form of quantum theory. The other is the geometrization of physical theories in almost every field. Here, of course, general relativity is only one particularly prominent example, but also the Yang-Mills theories for interactions in particle physics as well as the question of spinors lead in the end to new geometric formulations and insights. Topological properties also play an increasingly important role in, for example, solid state physics. For this reason, differential geometry is to be regarded as one of the important pillars of any modern physical theory and should therefore not be missing in any study of mathematical physics.

At Chair X, a basic knowledge of differential geometry is probably almost indispensable. Even for the more algebraic or functional-analytical problems at Chair X, differential geometry always provides the decisive examples, the motivation, and, finally, the intuition for what should actually be done. 

After the fundamental notions of differential geometry, the advanced lectures on geometric mechanics or on Pseudo Riemannschen and Riemannschen geometry, but also Analysis und Geometrie of Classical Systems, are of importance and interest for the work at Chair X. Finally, differential geometry is the starting point for various Research in Groups, student seminars and last but not least the master theses at Chair X.

Besides these aspects, however, there are also strong inner-mathematical reasons to deal with symplectic geometry. There are various applications in applied and pure mathematics, from particularly powerful numerical methods in the theory of ordinary differential equations like the symplectic integrators to deep applications in the representation theory of Lie algebras and Lie groups. Further, Kähler geometry provides a brigde from symplectic geometry to other areas of geometry such as Riemannian geometry or complex differential geometry.

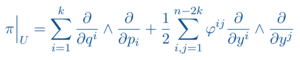
If one now puts the Poisson bracket of (geometric) Hamiltonian mechanics in the foreground, symplectic geometry generalizes to Poisson geometry: here one considers general manifolds with a Poisson bracket on the algebra of functions. Poisson geometry is by now a particularly active area in differential geometry, which in turn allows many applications in physics. In particular, field theories such as the Poisson sigma model should be mentioned here. But also in finite dimensions Poisson geometry plays a central role in various quantization theories.

At Chair X we work on various details in symplectic geometry and Poisson geometry. Although there are certainly alternative problems beyond symplectic geometry in our group, it is the case that all research directions are related to symplectic geometry in a more or less direct way. For this reason, after the lecture, there are regularly offered further Research in Groups in the area of symplectic geometry and Poisson geometry. They typically serve as agood starting point for master's theses.