Research Areas

Mathematical physics concerns itself with problems that are motivated by and have applications in various areas in physics. Accordingly, a plethora of mathematical techniques and fields of study, depending on the physical requirements, are employed.

Certainly, these fields contain the application oriented ones of mathematics: On the one hand, sophisticated statistical methods are needed to cope with the enormous datasets of modern physical experiments. On the other hand, physical issues have to be modelled and simulated, further demanding numerical and computational techniques from applied mathematics. Concrete examples are manifold.

Perhaps slightly less obvious is the central role of pure mathematics in mathematical physics. Numerous physical theories currently in discussion elude (at least for the time being) experimental validation. Nevertheless, one method of extracting meaning from such a theory is analyzing its conceptional structure. Here one quickly enters the realm of problems rooting deeply in pure mathematics. Some more renowned of them are of differential geometrical (classical geometric mechanics) of functional analytic (quantum mechanics) nature. But algebraic or even number theoretic considerations also have their part in comprehending modern physical theories.

What makes mathematical physics quite attractive is, for a start, the certainty of encountering non-trivial issues due to them emanating from physics and thus substanciating their relevance by posing concrete problems of the natural sciences. Furthermore, while pursuing issues in mathematical physics, one can draw from a multitude of mathematical fields of study. The latter is also of great inner-mathematical interest since significant advances often happen at the contact surface of different areas in mathematics. In this manner functional analytic issues in physics are viewed from a differential geometric perspective and rich algebraic structures are found in geometric problems which in turn lead to novel physical interpretations. Especially for mathematical physics, this interdisciplinary character is built into its very foundations, allowing a high flexibility as well as promoting the willingness to acquire ever new mathematical tools and disciplines, an inherent part in the daily life of every mathematical physicist.

The structural analysis of physical theories through mathematical physics also includes certain philosophical aspects: One is quickly led to questions concerning the evaluation of theories in the light of epistemology. Typical manifestations of them consider predictability, consistency and interpretation of mathematical models of physical theories.

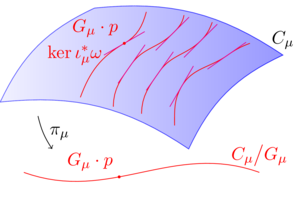
In symplectic geometry, one considers a manifold with a non-degenerate closed two-form, the symplectic form. On the one hand, this defines a musical isomorphism that allows one to obtain a vector field from the differential of a function, the Hamiltonian vector field of the function. On the other hand, the Hamiltonian vector fields of two functions can be paired with the symplectic form, which then provides a Poisson bracket due to the closedness of the form. These structures make it possible to formulate the basic equations of classical mechanics, the Hamilton equations of motion, in a geometrical way. Thus, the whole formalism of differential geometry is applicable to geometric mechanics.

A Poisson manifold generalizes this to the effect that arbitrary Poisson brackets are considered on the  algebra of functions, whether these brackets are non-degenerate or not. In this way one obtains substantially new  classes of examples. Poisson manifolds are by now the mathematical model of the phase space in classical mechanics and thus also the starting point for various quantization theories.

Lie groups are groups which additionally carry the structure of a differentiable manifold and are therefore well suited to describe symmetries in differential geometry. The possibility  to differentiate on a Lie group then yields the infinitesimal variant of the Lie group: its Lie algebra. The interplay of global information (Lie group) and the infinitesimal view (Lie algebra) is central to  Lie theory.

While Lie groups are already interesting on their own, the essential application in differential geometry is that they describe symmetries of geometric objects. To achieve this, we use the notion of group action on a manifold, which may then leave additional structures invariant. If there are enough symmetries such that the group action is even transitive, we speak of a homogeneous space. The study of those is  of fundamental importance for group actions, since each orbit of a group action is a homogeneous space, and the entire space is composed of the orbits.

Riemannian geometry is one of the classic areas in  differential geometry. Here, the metric geometry of a manifold is determined via a Riemann metric, i.e. a positive definite scalar product on each tangent space. In particular, it is possible to define geodesics, to determine distances and much more. However, Riemann metrics also occur in connection with other geometries, such as in Kähler geometry, or can be used as a tool in other areas of differential geometry.

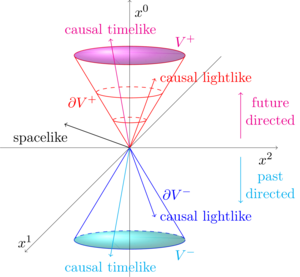
Lorentz geometry is the starting point for general relativity and can be seen as a time-dependent version of Riemannian geometry. In this framework, wave equations can be formulated in a geometrical way, whose initial value problems provide information about the underlying geometry. In recent years, there has been a rapid development, especially in conjunction with ideas from quantum field theory.

In generalized  geometry, the canonical Courant algebroid of a manifold is placed at the beginning of the considerations. Poisson structures as well as closed two-forms (pre-symplectic forms) are then uniformly described by Dirac structures in this Courant algebroid. In this way one obtains on the one hand a great unification, on the other hand many new examples of geometrical structures, which interpolate between symplectic and Poisson geometry.

The integrated or global version of the infinitesimal view then leads to the theory of Lie groupoids, which are equipped with additional structures depending on the generalized geometry.

Our group works mainly in pure mathematics with questions arising from classical geometric mechanics as well as quantum mechanics. In particular, we are interested in the transition from classical physics to quantum physics. Slightly un-precisely this is referred to as quantization, even though there are neither a commonly used way nor generally accepted requirements for such a quantization. This makes the topic an ideal area for mathematical physics which can help with a precise structural analysis of the physical ideas to extract the actual questions in a clear and precise way. Then suggestions for solutions can be formulated in terms of existence and classification results. Epistemic questions arise immediately: how much can be learnt from the understanding of classical models to yield the more realistic and actually realized quantum nature of the world. How many choices have to be made on the way, how many theoretical uncertainties can and have to be taken to obtain a still predictive description of nature.

The classical side is mainly modelled by differential geometric descriptions of geometric mechanics. The starting point is thus a symplectic manifold as phase space which encodes the kinematics of the classical system. Since at this stage the Poisson structure is the essential structural ingredient one can replace the symplectic manifold by a more general Poisson manifold. On the algebraic side the function algebra of (smooth) functions on a Poisson manifold becomes a Poisson algebra. This corresponds to the classical observable algebra.

To understand the quantum version of a classical system one also chooses the approach based on observable algebras. The quantum observable for a *-algebra which might be no longer commutative. Instead, the commutation relations between elements of the quantum observable algebra correspond to the experimentally found uncertainty relations. A purely algebraic description remains uncomplete since for quantum physics also the spectra of observables and the super position principle have be to implemented mathematically. To achieve this in a satisfactory way one needs various arts from functional analysis, in particular the theory of operator algebras. Ideally, one arrives at a C^*-algebra of observables at the end, together with a good understanding of its representation theory by operators on Hilbert spaces.

One possibility to obtain a candidate for the quantum observable algebra out of  the classical one is to deform the algebra product: here we use on the same underlying vector space of the classical observables a new, now  ℏ-dependent, non-commutative product. This should correspond now to the quantum mechanical multiplication law. The main advantage of this is that the physical interpretation of the observables on the quantum side is now trivially given: they are the very same observables as in the classical theory since we have the same elements of the same vector space. Note that this aspect of identifying the interpretation of an abstract algebra element as a given physical measurement procedure is typically rather non-trivial. It is not  that easy to say which operator on the quantum side corresponds to which physical observable, i.e. to which measurement apparatus. Nevertheless, the price for the deformation aspect is now that one has to understand this new multiplication, the star product.

The main requirements for a star product are now that it is associative since the operator multiplication certainly is. In addition one requires the correct classical limit for  ℏ = 0 where it should reduce to the classical, commutative product. In first order of  ℏ the commutator should yield the classical Poisson bracket. This is a compatibility owed to the time evolution which on the classical side is encoded by the Poisson bracket, on the quantum side by the commutator.

In deformation quantization the task is to model these physically motivated requirements on a mathematically sound basis. Here one has several approaches. The most simple is to find the star product as a formal power series in  ℏ. From the point of view of physics this can certainly not be the final solution. Nevertheless, it yields a mathematically manageable model.The discussion of the convergence properties of formal star products has to be postponed to a later stage. One can now analyse the existence and classification of such formal star products. Here one has by now a beautiful and far reaching theory: both, the existence and the classification of star products on general Poisson manifolds are well understood.