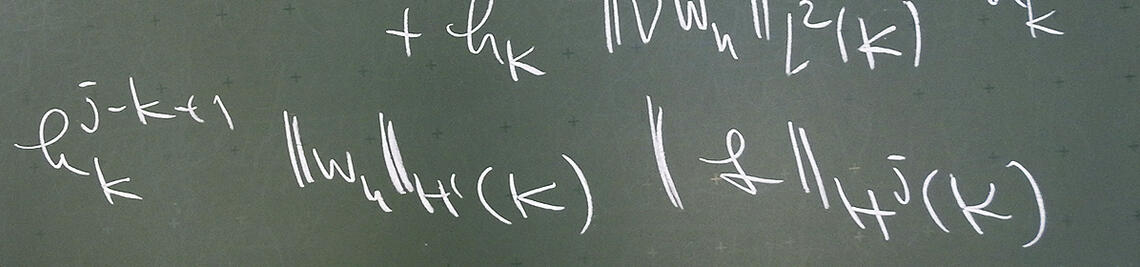English Intern
  • Mathematische Formel auf Tafel
  • Innenaufnahme der Teilbibliothek Mathematik
  • Nahaufnahme Notizen
Optimale Steuerung

Projekte

Optimization problems in fractional Sobolev spaces with application to sparse control problems

Collaboration partners

The project is a joint research project with Anna Lentz.

Project description

will follow

Funding

This project is funded by the German Research Foundation DFG under project grant Wa 3626/5-1.

  • 1.
    Spatially sparse optimization problems in fractional order Sobolev spaces
    Lentz, A., Wachsmuth, D.
    https://arxiv.org/abs/2402.14417 (2024)
  • 1.
    Control in the coefficients of an elliptic differential operator: topological derivatives and Pontryagin maximum principle
    Wachsmuth, D.
    Mathematical Control & Related Fields (2024)
  • 1.
    Capacitary measures in fractional order Sobolev spaces: Compactness and applications to minimization problems
    Lentz, A.
    https://arxiv.org/abs/2412.11876 (2024)
  • 1.
    Sparse optimization problems in fractional order Sobolev spaces
    Antil, H., Wachsmuth, D.
    Inverse problems 39, 044001 (2023)
  • 1.
    Strong stationarity for optimal control problems with non-smooth integral equation constraints: Application to continuous DNNs
    Antil, H., Betz, L., Wachsmuth, D.
    Appl. Math. Optim. 88, (2023)

Algorithms for Optimization Problems in Banach Spaces with Non-smooth Structure

Collaboration partners

The project is a joint research project with Christian Kanzow, Carolin Natemeyer and Bastian Dittrich.

Project description

The aim of this project is to develop and analyse algorithms for the numerical solution of some highly difficult optimization problems in Banach spaces. This includes mathematical programs with complementarity constraints,  switching constraints, or problems involving a sparsity term either in the objective function or the constraints. By exploiting the special structure of these problems, the goal is to derive solution methods with strong global and local convergence properties under realistic, problem-tailored assumptions. All methods will be implemented and tested extensively on several relevant examples.

Funding

This project is funded by the German Research Foundation DFG under project grant Wa 3626/3-2 within SPP 1962.

  • 1.
    Optimal control problems with L^0(Ω) constraints: maximum principle and proximal gradient method
    Wachsmuth, D.
    Comp. Opt. Appl. 87, 811-833 (2024)
  • 1.
    A topological derivative-based algorithm to solve optimal control problems with L^0(Ω) control cost
    Wachsmuth, D.
    J Nonsmooth Anal. Opt. 5, (2024)
  • 1.
    A numerical solution approach for non-smooth optimal control problems based on the Pontryagin maximum principle
    Wachsmuth, D.
    In: Gallego, R. and Mateos, M. (eds.) Proceedings of the French-German-Spanish Conference on Optimization (2024)
  • 1.
    The largest-K-norm for general measure spaces and a DC Reformulation for L^0-Constrained Problems in Function Spaces
    Dittrich, B., Wachsmuth, D.
    https://arxiv.org/abs/2403.19437 (2024)
  • 1.
    Non-monotone proximal gradient methods in infinite-dimensional spaces with applications to non-smooth optimal control problems
    Kanzow, C., Wachsmuth, D.
    (2023)
  • 1.
    Sparse optimization problems in fractional order Sobolev spaces
    Antil, H., Wachsmuth, D.
    Inverse problems 39, 044001 (2023)
  • 1.
    A Note on Existence of Solutions to Control Problems of Semilinear Partial Differential Equations
    Casas, E., Wachsmuth, D.
    SIAM J. Control Optim. 61, 1095-1112 (2023)
  • 1.
    A simple proof of the Baillon-Haddad theorem on open subsets of Hilbert spaces
    Wachsmuth, D., Wachsmuth, G.
    J. Convex Anal. 30, 1319-1328 (2023)
  • 1.
    Strong stationarity for optimal control problems with non-smooth integral equation constraints: Application to continuous DNNs
    Antil, H., Betz, L., Wachsmuth, D.
    Appl. Math. Optim. 88, (2023)
  • 1.
    A penalty scheme to solve constrained non-convex optimization problems in BV(Ω)
    Natemeyer, C., Wachsmuth, D.
    Pure Appl. Funct. Anal. 7, 1857–1880 (2022)
  • 1.
    Second-order conditions for non-uniformly convex integrands: quadratic growth in L^1
    Wachsmuth, D., Wachsmuth, G.
    J Nonsmooth Anal. Opt. 3, (2022)
  • 1.
    A proximal gradient method for control problems with non-smooth and non-convex control cost
    Natemeyer, C., Wachsmuth, D.
    Comp. Opt. Appl. 80, 639–677 (2021)
  • 1.
    Full stability for variational Nash equilibriums of parametric optimal control problems of PDEs
    Qui, N. T., Wachsmuth, D.
    http://arxiv.org/abs/2002.08635 (2020)
  • 1.
    First and second order conditions for optimal control problems with an L^0 term in the cost functional
    Casas, E., Wachsmuth, D.
    SIAM J. Control Optim. 58, 3486–3507 (2020)
  • 1.
    Iterative hard-thresholding applied to optimal control problems with L^0(Ω) control cost
    Wachsmuth, D.
    SIAM J. Control Optim. 57, 854-879 (2019)

Algorithms for Quasi-Variational Inequalities in Infinite-dimensional Spaces

Collaboration partners

The project is a joint research project with Christian Kanzow and Veronika Karl.

Project description

The aim of this project is to develop and analyse algorithms for the numerical solution of some classes of quasi-variational inequalities. Such inequalities occur, e.g., in connection with generalized Nash equilibria in multi-player control problems. Moreover, they are widely used to describe the value function in stochastic control problems. Our goal is twofold: (a) Transfer existing solution methods from finite-dimensional to infinite-dimensional problems. (b) Develop problem-tailored solution methods by taking into account the particular structure of certain quasi-variational inequalities. All methods should have a strong theoretical background and will be tested extensively on suitable examples.

Funding

This project is funded by the German Research Foundation DFG under project grant Wa 3626/3-1 within SPP 1962.

  • 1.
    Safeguarded augmented Lagrangian methods in Banach spaces
    Karl, V., Kanzow, C., Steck, D., Wachsmuth, D.
    In: Hintermüller, M., Herzog, R., Kanzow, C., Ulbrich, M., and Ulbrich, S. (eds.) Non-Smooth and Complementarity-Based Distributed Parameter Systems. pp. 241-282. Birkhäuser (2022)
  • 1.
    A Lagrange multiplier method for semilinear elliptic state constrained optimal control problems
    Karl, V., Neitzel, I., Wachsmuth, D.
    Comp. Opt. Appl. 831-869 (2020)
  • 1.
    On the uniqueness of non-reducible multi-player control problems
    Karl, V., Pörner, F.
    Optimization Methods and Software (2019)
  • 1.
    The multiplier-penalty method for generalized Nash equilibrium problems in Banach spaces
    Kanzow, C., Karl, V., Steck, D., Wachsmuth, D.
    SIAM J. Optim. 29, 767-793 (2019)
  • 1.
    An augmented Lagrangian method for optimization problems in Banach spaces
    Steck, D., Kanzow, C., Wachsmuth, D.
    SIAM J. Control Optim. 56, 272-291 (2018)
  • 1.
    An augmented Lagrange method for elliptic state constrained optimal control problems
    Karl, V., Wachsmuth, D.
    Comp. Opt. Appl. 69, 857-880 (2018)
  • 1.
    A joint Tikhonov regularization and augmented Lagrange approach for ill-posed state constrained control problems with sparse controls
    Karl, V., Pörner, F.
    Numer. Funct. Anal. Optim. 39, 1543-1573 (2018)

Regularization and Discretization of Inverse Problems for PDEs in Banach Spaces

Collaboration partners

The project is a joint research project with Dr. Frank Pörner, Christian Clason (Duisburg-Essen) and Barbara Kaltenbacher (Klagenfurt).

Project description

The aim of this project is a combined analysis of regularization and discretization of ill-posed problems in Banach spaces specifically in the context of partial differential equations. Such problems play a crucial role in numerous applications ranging from medical imaging via nondestructive testing to geophysical prospecting, with the Banach space setting mandated by the inherent regularity of the sought coefficients as well as structural features such as sparsity.

Funding

This project is funded by the German Research Foundation DFG under project grant Wa 3626/1-1.

  • 1.
    On the uniqueness of non-reducible multi-player control problems
    Karl, V., Pörner, F.
    Optimization Methods and Software (2019)
  • 1.
    Iterative hard-thresholding applied to optimal control problems with L^0(Ω) control cost
    Wachsmuth, D.
    SIAM J. Control Optim. 57, 854-879 (2019)
  • 1.
    Second-order analysis and numerical approximation for bang-bang bilinear control problems
    Casas, E., Wachsmuth, D., Wachsmuth, G.
    SIAM J. Control Optim. 56, 4203-4227 (2018)
  • 1.
    Error estimates for the approximation of a discrete-valued optimal control problem
    Clason, C., Do, T. B. T., Pörner, F.
    Comp. Opt. Appl. 71, 857-878 (2018)
  • 1.
    Regularization Methods for Ill-Posed Optimal Control Problems
    Pörner, F.
    http://nbn-resolving.org/urn:nbn:de:bvb:20-opus-163153 (2018)
  • 1.
    A priori stopping rule for an iterative Bregman method for optimal control problems
    Pörner, F.
    Optimization Methods and Software 33, 249-267 (2018)
  • 1.
    A joint Tikhonov regularization and augmented Lagrange approach for ill-posed state constrained control problems with sparse controls
    Karl, V., Pörner, F.
    Numer. Funct. Anal. Optim. 39, 1543-1573 (2018)
  • 1.
    Inexact Iterative Bregman Method for Optimal Control Problems
    Pörner, F.
    Numerical Functional Analysis and Optimization 39, 491-516 (2018)
  • 1.
    Stability for bang-bang control problems of partial differential equations
    Qui, N. T., Wachsmuth, D.
    Optimization 67, 2157-2177 (2018)
  • 1.
    Tikhonov regularization of optimal control problems governed by semi-linear partial differential equations
    Pörner, F., Wachsmuth, D.
    Mathematical Control & Related Fields 8, 315-335 (2017)
  • 1.
    Sufficient second-order conditions for bang-bang control problems
    Casas, E., Wachsmuth, D., Wachsmuth, G.
    SIAM J. Control Optim. 55, 3066-3090 (2017)
  • 1.
    On the switching behavior of sparse optimal controls for the one-dimensional heat equation
    Tröltzsch, F., Wachsmuth, D.
    Mathematical Control & Related Fields 8, 135-153 (2017)
  • 1.
    An iterative Bregman regularization method for optimal control problems with inequality constraints
    Pörner, F., Wachsmuth, D.
    Optimization 65, 2195-2215 (2016)
  • 1.
    A sharp regularization error estimate for bang-bang solutions for an iterative Bregman regularization method for optimal control problems
    Pörner, F.
    In: Proceedings in Applied Mathematics and Mechanics. pp. 787-788 (2016)
  • 1.
    Functional error estimators for the adaptive discretization of inverse problems
    Clason, C., Kaltenbacher, B., Wachsmuth, D.
    Inverse Problems 32, 104004 (2016)

Higher-order finite elements for optimal control problems

Collaboration partners

The project is a joint research project with Sven Beuchler (Bonn).

Project description

The mathematical models of many technical processes contain partial differential equations. Here, it is important to optimize these processes. Often the optimization variables are subject to constraints that have to be taken into account. As model problem, consider the minimization of a functional

g(y)+j(u)
subject to the elliptic equation
-Δy =u on Ω,   y=0 on Γ
and pointwise control
ua ≤ u ≤ ub
and state constraints
ya ≤ y ≤ yb

The numerical solution of this problem offers many challenges. One of them is the low regularity of Lagrange multipliers associated to the state constraints, which are measures. The global regularity of the solution of the optimal control problem is limited by quantities that have small support.
The project will exploit this property and develop methods for an adaptive hp-discretization of the optimal control problem, where the solution is approximated by high-order polynomials on large triangles where it is smooth, whereas the solution is approximated by low-order polynomials on small triangles in regions, where it is non-smooth.

Funding

This project was funded by the Austrian Research Fund FWF under project grant P23484.

Numerical verification of optimality and optimality conditions for optimal control problems

Project description

Many technical processes are described by partial differential equations. Here, it is important to optimize these processes. This leads to optimization problems in an infinite-dimensional setting.
As model problem, consider the minimization of a functional

g(y)+j(u)
subject to the elliptic equation
-Δy + d(y)=u on Ω,   y=0 on Γ
and pointwise control constraints
ua ≤ u ≤ ub

Despite its simple structure, this problem offers many difficulties and challenges. Due to the non-linear elliptic equation this optimisation problem becomes non-convex.
If one has computed solutions yh and uh of discretized versions of this problem, the question arises

Are yh and uh indeed an approximation of a solution of the infinite-dimensional problem?

Due to the inherent non-convexity of the optimization problem, this question is by far non-trivial. The project wants to give answers to this question with information that is computable from the numerical solution. The methods that will be applied are based on techniques from optimal control, finite element methods, and eigenvalue computations.

Funding

This project was funded by the Austrian Research Fund FWF under project grant P21564.