Research areas
Mathematical Fluid Mechanics
theory of hyperbolic conservation laws
- towards a proper solution concept for the multi-dim. compressible Euler equations
- convex integration, non-uniqueness for the multi-dim. compressible Euler equations
structure preserving numerical schemes for Euler and ideal magnetohydrodynamics
- well-balanced and low Mach schemes for Euler equations with gravity
- genuinely multi-dim. schemes
- structure-preserving compact high-order method method
applications in astrophysics
- numerical schemes for evolving stellar structure and evolution
- simulations of the evolution of the universe including magnetic fields
kinetic equations and plasma, theory & numerics
- multi-species models, existence and qualitative behavior
- numerical schemes for multi-species BGK equations based on a variational procedure
PDE inverse problems, kinetic models in biology with coefficients determined by experimental data
- theory: proving that it is possible to solve certain kinetic PDE inverse problems
- numerics: schemes that determine the coefficients from given experimental data
Further information on the areas of research here
I'm a PhD student working on developing and implementing numerical methods for conservation laws. My primary interests are in developing moving mesh methods for compressible flows in multiple dimensions. I also work on porous media flows in one dimension and uncertainty quantification for the same. My other interests are in writing efficient, parallelized and reproducible code for the aforementioned numerical methods.
Various natural phenomena can be described using partial differential equations (PDEs). They often contain parameters that fit the general description of the phenomenon to a concrete situation. Reconstructing these parameters from experimental data is called the inverse problem and is necessary to fit the model and to enable prognosis.
I investigate such a parameter identification problem for a model of bacterial motion stimulated by a chemical signal (like a food source), which is called chemotaxis. It is often modelled by a kinetic chemotaxis equation in which a parameter encodes the bacterial reaction to the chemical signal. Supposing to be given velocity independent measurements of the bacteria density, photographies for instance, I study whether such data can contain enough information to recover the kinetic parameter. Furthermore, I study the relation between the reconstruction from the kinetic and a corresponding macroscopic Keller-Segel model.
The main goal of my research is the numerical solution of inverse problems on a kinetic level. To this end, we want to use the interplay between kinetic and macroscopic models. Further, we want to make this process more efficient by incorporating reduced order approaches such as low-rank approximation.: The main goal of my research is the numerical solution of inverse problems on a kinetic level. To this end, we want to use the interplay between kinetic and macroscopic models. Further, we want to make this process more efficient by incorporating reduced order approaches such as low-rank approximation.
The partial differential equations (PDEs) which appear in mathematical fluid mechanics describe the time evolution of a fluid. One expects that repeating a particular experiment with a real fluid several times always leads to the same observation. This fact should be recovered in terms of uniqueness of the solution to the underlying mathematical model (i.e. the corresponding PDE). However, for many fluid models one can construct infinitely many solutions to given initial datum using a method called "convex integration". This non-uniqueness questions the solution concept which is used here (so-called weak entropy solutions).
Moreover, the conjecture by Onsager, which comes from turbulence theory, was proven for incompressible fluids using convex integration. This indicates that there is a relation between non-uniqueness and turbulence.
The Goal of my research is to find a suitable solution concept, in particular in view of turbulent flows. This leads to the question whether the notion of a weak solution can be retrieved by imposing an additional criterion which singles out one solution among the infinitely many. Or if one has to consider a generalized notion of solution instead (e.g. measure-valued solutions).
Many fluid mechanical problems can be described using hyperbolic systems of conservation laws, such as the Euler equations. The numerical solution of these conservation laws often involves the use of Finite Volume or Discontinuous Galerkin methods. The Active Flux method combines both schemes using a continuous solution reconstruction in the considered domain. My work deals with the further development of a generalized Active Flux scheme. In particular, this scheme allows to solve conservation laws in multiple dimensions with arbitrarily high order. It is expected that this numerical method exhibits many structure preserving properties (e.g. preserving positivity, high fidelity for vortices, low Mach number compliance for the compressible Euler equations).
My research topic is in the area of modelling and mathematical theory for kinetic equations. I want to develop models for applications describing for example a plasma, a gas mixture with chemical reactions or the spread of aerosols. Then I underpin this models with proving in a mathematical way physical properties of the solution (entropy inequality, large-time behaviour, limit to macroscopic equations) and also mathematical properties like existence and uniqueness of solutions.
Kinetic equations describe the mesoscopic behaviour of fluids. New models are developped including more physical properties. Finally, the equations are solved numerically. I work on the numerics of a multi-species BGK-model.
My topic of research is asymptotic preserving schemes that are stationary preserving. In this project we are curious about the relationship between asymptotic preserving schemes and stationary preserving ones. For this purpose, we picked up a well-known asymptotic preserving scheme and proved it stationary preserving as well. From the way we used to prove the stationary preserving property, we are trying to find a general concept or at least cases where one can generalize that every asymptotic preserving scheme is stationary preserving.
What I do:
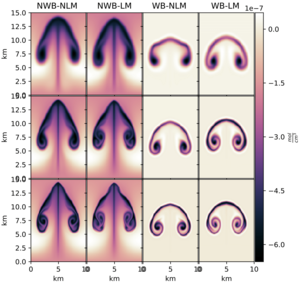
I am working on finite volume numerical methods for hyperbolic systems. Especially, I am considering compressible Euler and magnetohydrodynamics equations with gravity source term, for which I construct well-balanced methods and low Mach numerical fluxes.
What I tell non-mathematicians when they ask what I do:
Astrophysicists are interested in how the gas in the interior of stars are moving. For this they do computer simulations. Unfortunately, conventional simulation methods for this application tend to fail in two crucial points: Firstly, these methods are not able to even maintain the basic structure of the star, such that the gas is falling to the center of the star of moving away from it, which is not correct. Secondly, it is especially hard to simulate slow motions of the gas. I am trying to develop methods which can solve these problems.
In my research I focus on the development of numerical methods to simulate fluid dynamical processes in the context of astrophysical phenomena. These include the simulation of stellar atmospheres and gas flow in glactic disks. The numerical methods used in my research include Finite-Volume and Discontinous Galerkin methods. In this context I design Well-Balanced and Asypmtotic-Preserving methods to cope with the challanges in the prescribed flow regimes. Moreover I specialize in the application of the relaxation technique to develope robust and stable schemes.