Fokker-Planck Equations
Fokker-Planck Equations and Optimal Control of Stochastic Processes
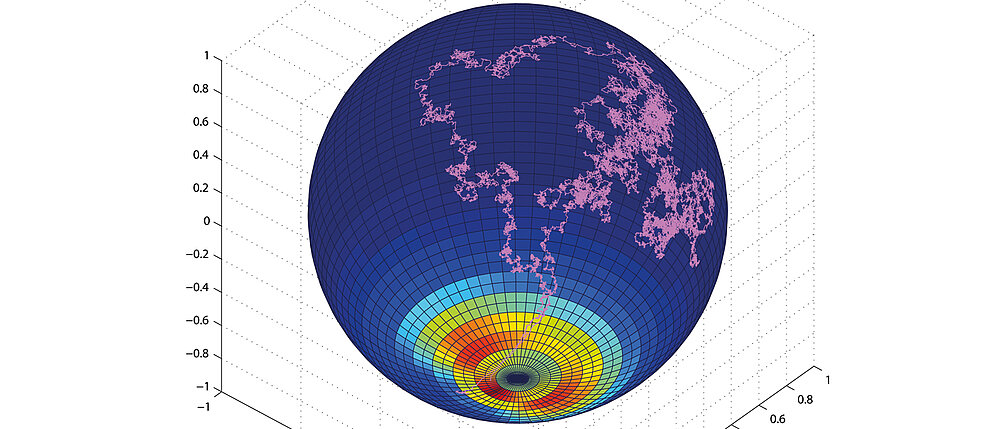
We work on the development of a new framework for the optimal control of probability density functions (PDF) of stochastic processes. This framework is based on Fokker-Planck (FP) partial differential equations that govern the time evolution of the PDF of stochastic systems and on control objectives that may require to follow a given PDF trajectory or to minimize an expected-value functional. Corresponding to different stochastic processes, different FP equations are obtained. In particular, FP equations of parabolic, fractional parabolic, integro parabolic, and hyperbolic type appear. The corresponding optimization problems are deterministic and can be formulated in an open- or closed-loop framework. In fact, the FP control approach allows to derive the Hamilton-Jacobi-Bellman equation and to consider the dynamic programming principle from another viewpoint. Stochastic processes appear in many applications in biology, economics, finance, physics, etc., and so the FP control framework has large applicability.