Multigrid Methods
Multigrid Methods for Partial Differential Equations and PDE Optimization
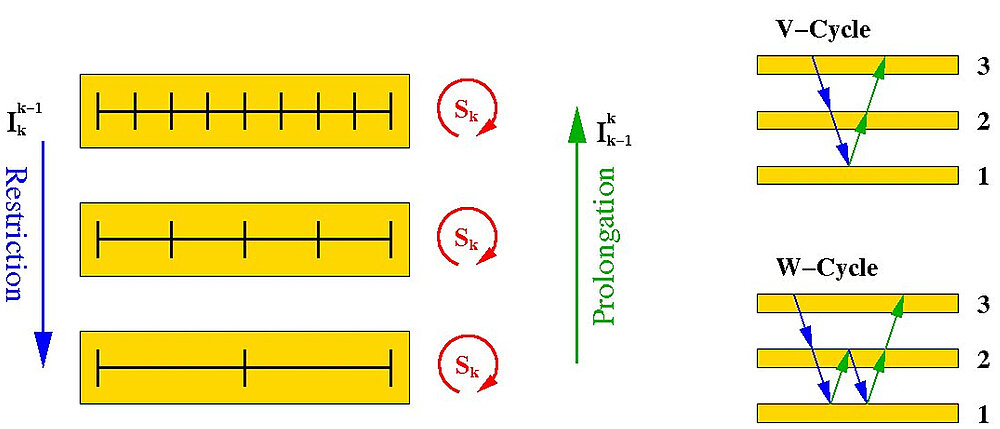
Multilevel strategies originate from the methodology of viewing a problem as having different characteristic length-scales, and based on this paradigma develop and combine numerical solution schemes that are effective on these scales in such a way to obtain fast and accurate solution procedures to the original problem. In this framework, multilevel (or multigrid) methods apply to many classes of linear and nonlinear algebraic and functional problems. Our focus is the development and analysis of multilevel methods for solving unconstrained and constrained optimization problems governed by partial differential equations (PDEs). These problems arise in many application fields as PDE control and inverse problems, shape optimisation, etc.
Projects:
SFB Austria: MGINV - Fast Multigrid Methods for Inverse Problems