Mehrgitterverfahren

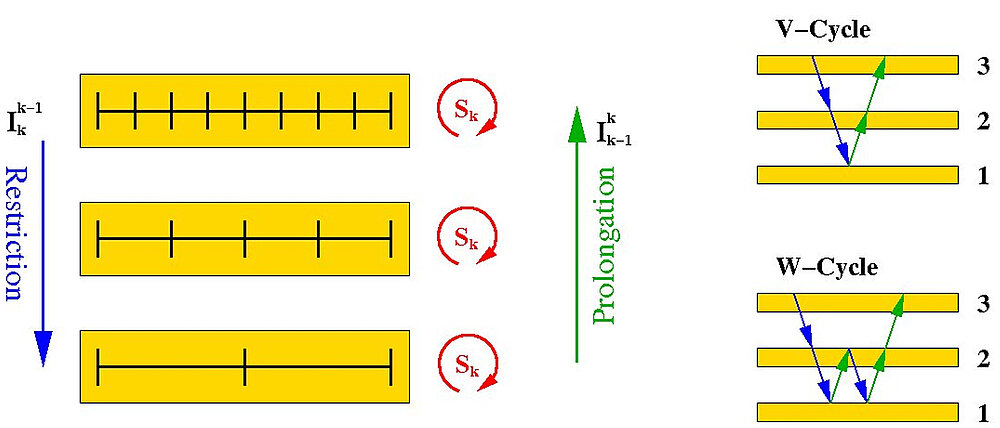
Mehrgitterverfahren stammen aus der Methodik der Betrachtung eines Problems als ob man unterschiedliche charakteristische Längenskalen hat. Sie entwickeln und kombinieren, basierend auf diesem Paradigma, numerische Lösungsschemata, die auf diesen Skalen in der Art wirksam sind, dass man schnelle und genaue Lösungsverfahren für das ursprüngliche Problem erhält. In diesem Rahmen sind mehrstufige (oder mehrgittrige) Methoden für viele Klassen von linearen und nichtlinearen algebraischen und funktionalen Problemen anwendbar. Unser Schwerpunkt liegt in der Entwicklung und Analyse von mehrstufigen Methoden zur Lösung von uneingeschränkten und eingeschränkten Optimierungsproblemen, die durch partielle Differentialgleichungen (PDEs) gesteuert werden. Diese Probleme entstehen in vielen Anwendungsbereichen wie PDE-Kontrolle und inverse Probleme, Formoptimierung, etc.

Projekte:

• SFB Austria: MGINV - Fast Multigrid Methods for Inverse Problems

Publikationen