Projekte
Projektleitung: PD Dr. habil. Anton Klimovsky mit Prof. Dr. Lisa Hartung (Universität Mainz)
Förderinstitution: DFG
Förderkennzeichen: 443891315, Teilprojekt im SPP 2265: Zufällige geometrische Systeme
Projektlaufzeit: 2020-2026
Projektbeschreibung: Wie wirkt die Raumzeit variierende Umgebung auf das Langzeitverhalten der räumlich strukturierter Populationen wechselwirkender Partikeln/Individuen/Agenten aus? Diese Frage ist von hoher Relevanz, z.B. in den Lebens-/Sozial-/Wirtschaftswissenschaften, der Informatik und der künstlichen Intelligenz. Aus mathematischer Sicht konzentriert sich das Projekt auf zwei phänomenologische Modelle wechselwirkender Partikelsysteme: (1) die verzweigende Brownsche Bewegung, die das Wachstum/die räumliche Ausbreitung einer Population modelliert, und (2) das Wählermodell, das den Informationsaustausch in einer Population modelliert. Die neuen Merkmale, die dieses Projekt in diese klassischen Modelle einführt, sind (1) raum-zeitkorrelierte Umgebungen und (2) evolvierende Netzwerke. Diese übernehmen die Rolle der geografischen Räume, deren zugrundeliegende Geometrie durch die zufälligen Strukturen stark beeinflusst wird. Das Projekt zielt darauf ab, (1) Wachstum/Aussterben, Populationsgröße, räumliche Ausbreitung der Agenten; und (2) Clustering gegenüber Konsens von Agentenzuständen sowie Raum-Zeit-Skalierungslimiten stochastischer Prozesse auf Netzwerken zu untersuchen.
Projektleitung: Prof. Dr. Markus Bibinger
Mitarbeiter: Malon Jansen, Michael Sonntag
Kooperationspartner: Prof. Dr. Moritz Jirak (Universität Wien)
Projektlaufzeit: 2018-2023
Förderinstitution: DFG
Förderkennzeichen: 403176476
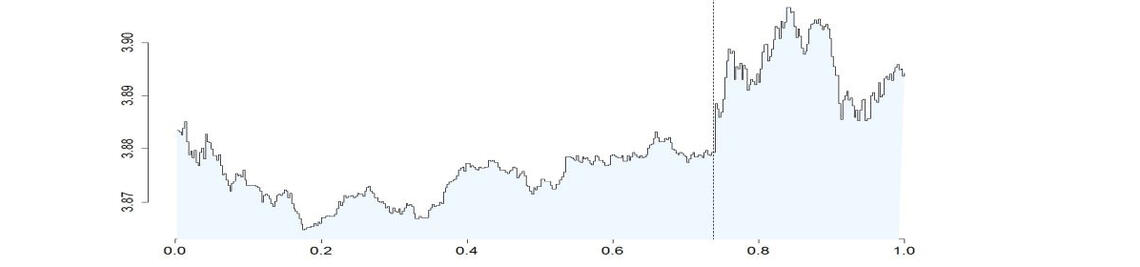
Projektbeschreibung: In diesem Projekt wird eine Theorie entwickelt, die statistische Inferenz über Pfadeigenschaften der Volatilität ermöglicht. Volatilität ist die zentrale Größe, um Unsicherheit in der Entwicklung von stochastischen Prozessen zu beschreiben. Im Besonderen bestimmen ihre Pfadeigenschaften optimale Schätz- und Prognosemethoden sowie die Persistenz der Volatilität.Trotz der großen Wichtigkeit der Pfadeigenschaften der Volatilität für Anwendungen gibt es Abseits einiger empirischer Arbeiten kein mathematisches statistisches Fundament. In der jüngeren Vergangenheit gab es grundlegende Beiträge zu Pfadeigenschaften von Prozessen, die direkt beobachtet werden. Der große Unterschied, woraus sich das Hauptproblem ableitet, ist, dass Volatilität ein impliziter Prozess ist und daher nicht direkt beobachtet werden kann. In einer ersten gemeinsamen Arbeit mit Prof. Jirak haben wir dieses Problem mittels Statistiken basierend auf Vorschätzungen untersucht. Der Fokus lag hierbei auf Strukturbrüchen der Pfadeigenschaften. Indem wir die neuesten Beiträge zur Schätzung der Volatilität aus Hochfrequenzdaten mit denen zur Inferenz über Pfadeigenschaften aus direkten Beobachtungen kombinieren, wollen wir erstmalig Inferenz für Pfadeigenschaften eines latenten Prozesses erreichen.
Die aktuelle Literatur präsentiert widersprüchliche Modelle für Volatilität, die unterschiedliche Faktoren berücksichtigen. Um diese Widersprüche zu lösen, sind mehr Informationen über die Pfadeigenschaften nötig. Die Theorie, die in diesem Projekt entwickelt wird, ist invariant bezüglich dieser Faktoren, und ermöglicht daher Aussagen über Pfadeigenschaften für alle gängigen Volatilitätsmodelle. Zusätzlich können auch zeitlich variierende Pfadeigenschaften erkannt werden. Das Projekt ist von besonderem Interesse für die Finanzmarktökonometrie, da verlässliche Volatilitätsmodelle Schlüsselelemente der Risikoanalyse sind. Unser Hauptinteresse gilt Hochfrequenzdaten, da fast 70% des Handelsvolumens durch Hochfrequenzhandel entsteht. Allerdings muss deren Marktmikrostruktur berücksichtigt werden, die zu Modellen mit verrauschten Preis-Beobachtungen führt. In diesem Projekt behandeln wir zwei allgemeine Rausch-Modelle: Das klassische zentrierte „Market Microstructure Noise“-Modell, und ein nicht reguläres Rausch-Modell, welches das Verhalten von Preisen in einem Limit Order Book modelliert. Das Projekt widmet sich den unterschiedlichen Modellen in drei Teilbereichen. Einer wird von Prof. Bibinger und Prof. Jirak bearbeitet und soll wichtige statistische Grundlagen liefern. Dabei wird in einem idealisierten Modell die minimal notwendige Information bestimmt, um qualitative Aussagen über die Pfadeigenschaften zu treffen. Die Projekte der Mitarbeiter behandeln neue optimale Methoden für die beiden verschiedenen Mikrostruktur-Modelle. Die kompliziertere Struktur in diesen realistischeren Modellen verlangt anspruchsvolle Techniken, um die Pfadeigenschaften der Volatilität zu bestimmen und zu klassifizieren.
Projektleitung: PD Dr. habil. Anton Klimovsky
Förderinstitution: DFG
Förderkennzeichen: 412848929
Projektlaufzeit: 2019-2022
Informationen: Siehe Homepage.
Projektbeschreibung: In den letzten 20 Jahren wurden komplexe Netzwerke zu einem Schlüsselwerkzeug für das Modellieren der komplexen Systemen in den Wissenschaften. Allerdings verändern sich viele Netzwerke im Laufe der Zeit und dies kann erhebliche Auswirkungen auf die Prozesse haben, die sich auf ihnen entfalten. Darüber hinaus kann der Einfluss auch umgekehrt sein: Prozesse, die auf einem Netzwerk stattfinden, können Auswirkungen auf die Topolgie des Netzwerks selbst haben. Dieses Phänomen führt zu sogenannter Koevolution in adaptiven Netzwerken (oder allgemeiner in komplexen adaptiven Systemen). Beispiele hierfür sind unter anderem epidemiologische, ökologische, neuronale, systembiologische und soziale Netzwerke, Finanzmärkte usw. In all diesen Kontexten herrscht eine große Unsicherheit über die Struktur und Dynamik des komplexen Systems.Was sind die aufkommenden globalen Muster in komplexen Systemen? Wie kommen sie aus dem Verhalten der Elemente zustande? Dies sind typische Fragen in den Wissenschaften, Wirtschaft und Politikgestaltung. Diese Fragen führen sofort zu schweren mathematischen Problemen über die Modelle komplexer Systeme, aber auch über deren Beziehungen zu den komplexen Daten.Das Ziel dieses wissenschaftlichen Netzwerkes ist die rigorose mathematische Theorie stochastischer Prozesse auf (ko)evolvierenden Netzwerken voranzutreiben.Das wissenschaftliche Netzwerk konzentriert sich auf:(a) Die probabilistischen Grundlagen stochastischer Prozesse auf (ko)evolvierenden Netzwerken.(b) Analyse und Synthese von Schlüsselbeispielen aus den Bereichen Informationsaustauschprozesse, Populationsdynamik, Infektionsprozesse und Dynamik von künstlichen neuronalen Netzwerken.(c) Fragen der statistischen Inferenz, Schätzung und Unsicherheitsquantifizierung für (evolvierende) komplexe Netzwerke und Prozesse auf ihnen.