Research Areas

The research by Markus Bibinger and his group is devoted to statistics for stochastic processes. Stochastic processes are used to model dynamic quantities which change over time. The theory of stochastic processes focusses in particular on continuous-time processes whose realizations are functions ("paths"). Statistics for stochastic processes allows to calibrate models to data and can be used for applications. Typically, the data is described by discrete observations of a continuous-time process.
The continuous-time nature of the model is nevertheless crucial, since the dynamics take place in continuous time and one can consider various discretization schemes.In statistics we aim to construct optimal hypothesis tests and efficient estimators for parameters or functions. For instance, we are currently investigating which path properties, as regularity, can be identified based on discrete observations and how to perform inference on them in an optimal way.

Within the DYNSTOCH network we have a regular exchange of the international community working on this research field which stimulates many collaborations. The annual conference of this network provides a platform, for young researchers to get in touch with leading international experts.

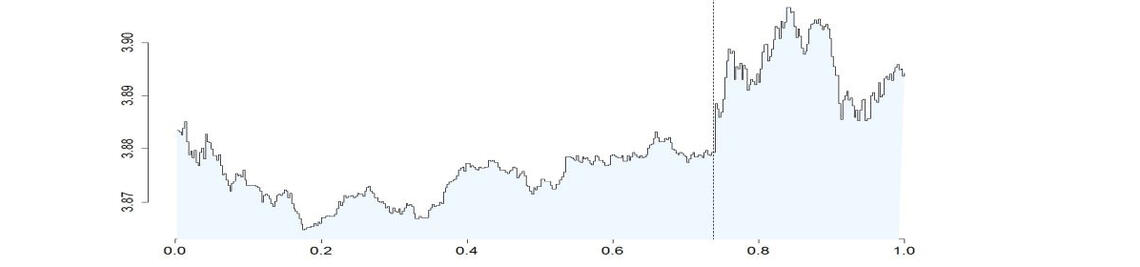
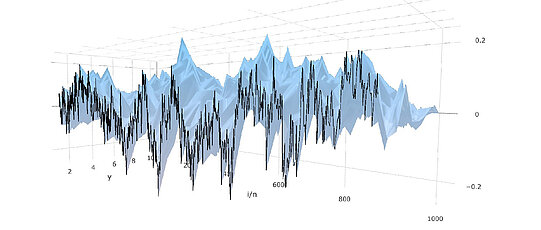
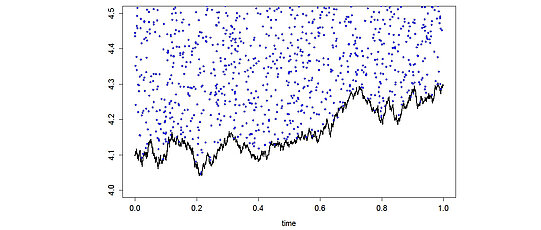
We work on applications of statistics for processes in financial econometrics. We are especially interested in intra-day, high-frequency financial data. For many liquid financial instruments huge numbers of observations are nowadays available ("big data"). In a limit order book, often several price recordings per second are available. Modelling and analysis of such high-frequency financial data becomes more and more important as much volume, currently almost 70%, is attributed to high-frequency trading. Mathematical finance, with the theory of efficient markets and no arbitrage considerations,
motivates to use semi-martingales as stochastic processes to model logarithmic price evolutions. One characteristic of these semi-martingales is the volatility which reflects intrinsic risk due to price oscillations. In the multi-dimensional case, a volatility matrix includes as well the complete
portfolio correlation structure. Additionally, jump components of semi-martingales can model large, sudden price changes as response to news and shocks. Price data recorded at very high frequencies is affected by market microstructure noise, such that we require more complex observation models with noise. The estimation of volatility and techniques to separate noise, jumps and continuous price movements in such models are subject of our research.

The methods have been applied, for instance, to distinguish systemic and idiosyncratic risk factors. In a collaboration with Lars Winkelmann from FU Berlin and researchers at the European central bank, we used high-frequency prices of different government bonds to analyze and compare instruments of communication and market guidance. To analyze systemic risk factors in large portfolios we currently begin to develop a theory on statistics for high-dimensional, high-frequency financial data.