ML irrational
Onlinematerialien zum Beitrag
Schau mal an: Wie zufällig ist Pi? (ML 208)
Im Beitrag wird der Frage nachgegangen: Wie „zufällig“ sind denn die Nachkommastellen von Pi oder von Wurzel(2) wirklich? Dazu werden qualitative geometrische Betrachtungsweisen als Visualisierungsvariante verwendet.
Mit denselben Verfahren lassen sich auch andere Zahlen untersuchen. Wir fragen daher allgemeiner – sind irrationale Zahlen generell als Quelle quasi-zufälliger Nachkomma-Folgen geeignet? Und wie unterscheiden sie sich in dieser Darstellungsweise von rationalen Zahlen?
Sie finden hier die nötigen Werkzeuge zum Experimentieren und Erforschen von Nachkommaziffernmustern.
Muster erkunden
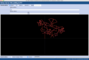
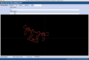
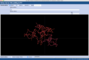
Nachkommastellen von irrationalen oder von rationalen Zahlen als Zick-Zack-Linie oder "genordete Kompassnadel" (siehe Beitrag) darzustellen, offenbart - wo vorhanden - Regelmäßigkeiten und Muster. Wir haben hier einige für Sie zusammengestellt:
Im obigen Video werden die rationalen Zahlen der Form 1/n (Stammbrüche) wie im Beitrag beschrieben dargestellt, wobei n von 1 bis 499 läuft.
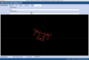
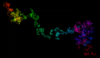
Der "Drache": 1/491
Einige rationale Zahlen bilden ganz besondere Formen. Im obigen Video sehen Sie beispielsweise, wie sich 1/491 langsam zu einer symmetrischen, geschlossenen Figur entwickelt, die an einen Drachen erinnert.
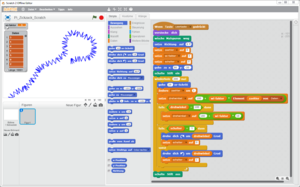
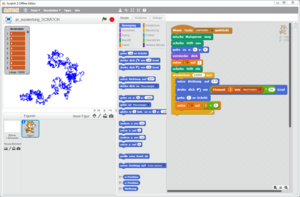
Variante I: Zick-Zack-Linien mit Scratch
Als eine Variante zur Erkundung der Eigenschaften von Nachkommastellen, wird im Beitrag die Verwendung der Programmierumgebung Scratch vorgeschlagen. Sie können die Software hier herunterladen oder online nutzen:
Ein geeignetes Scratch-Programm können Sie mittels Drag-and-Drop selbst zusammenstellen oder hier herunterladen:
Beliebige Folgen von Nachkommastellen lassen sich als Listen (Dateiobjekt: Daten) in Scratch importieren, sofern jede Ziffer in einer eigenen Zeile in einer txt-Datei steht. Einige Beispieldateien, die Sie in unser Beispielprojekt einfügen können, finden Sie im Downloadbereich.
Variante II: Scratch mit Nachkomma-Kompass
Die oben vorgestellte Scratch-Variante lässt sich leicht zu einer Variante erweitern, in der die Nachkommastellen entlang eines "Nachkomma-Kompass" (vgl. Abb. 13 des Beitrags) angeordnet werden. Ein Beispielprojekt finden sie hier:
Downloads zum Beitrag: Auswertung mit Scratch
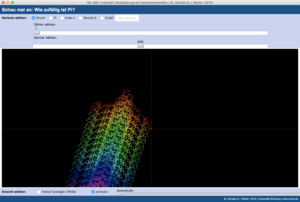
Variante III: irrationale vs rationale Zahlen mittels Tool
Um den Vergleich einiger irrationaler Zahlen mit rationalen Zahlen in der beschriebenen Visualisierungsform flexibel und rasch durchführen zu können, kann man die Scratch-Varianten in andere Programmiersprachen überführen. Wir haben dies für Sie in Python umgesetzt; das Ergebnis ist als "irrational-Tool" hier zum Download verfübar:
- irrational-Tool (exe) für Windows
- irrational-App (dmg) für MacOS
Sie haben die Wahl zwischen diesen Dezimalziffern-Folgen:
- Brüche der Form m/n, wobei m aus {1,...,100} und n aus {1,...,1000}
- Pi
- Eulersche Zahl e
- Wurzel(2)
- Zufallsfolge
Darstellungsvarianten:
- Schwarz/Weiß
- bunt
- mit oder ohne Verlauf