Turm von Hanoi - Mathematische Hintergründe
Die Anzahl der benötigten Spielzüge beim Spiel „Turm von Hanoi“ entspricht einer Folge. Jeder Anzahl von Scheiben wird dabei durch eine Zuordnungsvorschrift eine bestimmte Anzahl an Spielzügen zugeordnet.
Scheiben | 1 | 2 | 3 | 4 | 5 | … | 10 |
Spielzüge | 1 | 3 | 7 | 15 | 31 |
| 1023 |
Es gibt verschiedene Möglichkeiten, die Anzahl der benötigten Spielzüge zu bestimmen:
- durch eine Formel (explizit)
- durch eine rekursive Vorschrift
Beim Turm von Hanoi kann die Anzahl der Spielzüge für beliebig viele Scheiben über die Formel errechnet werden.
Bei der rekursiven Vorschrift wird das nächste Folgenglied aus den vorherigen Folgegliedern ermittelt. Um die Anzahl der Spielzüge für den nächst größeren Turm zu ermittelt, wird die Anzahl der benötigten Spielzüge verdoppelt und eins addiert.
Alternativ kann die Differenz der Anzahl der Spielzüge erforscht und zur weiteren Berechnung genutzt werden. Dabei lässt sich feststellen, dass die Differenz den Zweierpotenzen (2, 4, 8, …) entspricht. Für die Freunde der Mathematik gibt es auch hier eine Formel: .
Zunächst muss der vorherige Turm umgesetzt werden (rote Zahlen), anschließend wird die größte Scheibe (grüne Zahl) verlegt. Nun muss der vorherige Turm wieder auf diese zurückgesetzt werden (blaue Zahl).
Dieser Zusammenhang kann von einigen Kinder selbst formuliert und von den meisten Kinder problemlos nachvollzogen werden.
Diese Differenz lässt sich gut durch Pfeile veranschaulichen. Während Erwachsene in den Zahlen schnell die Zweierpotenzen erkennen, Formulieren Kinder den Zusammenhang als Verdoppelung der vorherigen Zunahme. Beide Möglichkeiten sind identisch und richtig.
Ausgehend von der Berechnung der Spielzüge können weitere Überlegungen hinsichtlich der Dauer des Umlegens angestellt werden. In diesem Sinne bietet die Aufgabe zusätzlich zum Problemlösen, Argumentieren, Kommunizieren und Darstellen auch die Möglichkeiten zum Modellieren. Es werden Vereinbarungen zur benötigten Zeit gemacht und zur dann zur Berechnung genutzt.
Für die in der Legende (vgl. unterrichtliche Ideen) beschriebene Ausgangssituation werden damit insgesamt 18 466 744 073 709 551 615 (ca. 18,5 Trillionen) Spielzüge benötigt. Verschieben die Priester im Tempel die Scheiben Tag und Nacht und benötigen dabei pro Zug 1 Sekunde, vergehen über 580 Milliarden Jahre bis der Turm komplett umgelegt wurde. Hätten Sie mit diesem Ergebnis gerechnet?
Die folgende Tabelle zeigt die Überlegung anschaulich:
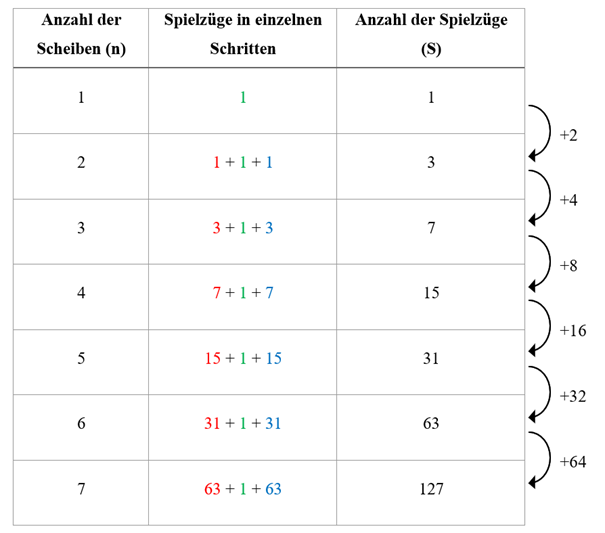
Zunächst muss der vorherige Turm umgesetzt werden (rote Zahlen), anschließend wird die größte Scheibe (grüne Zahl) verlegt. Nun muss der vorherige Turm wieder auf diese zurückgesetzt werden (blaue Zahl).
Dieser Zusammenhang kann von einigen Kinder selbst formuliert und von den meisten Kinder problemlos nachvollzogen werden.
Diese Differenz lässt sich gut durch Pfeile veranschaulichen. Während Erwachsene in den Zahlen schnell die Zweierpotenzen erkennen, Formulieren Kinder den Zusammenhang als Verdoppelung der vorherigen Zunahme. Beide Möglichkeiten sind identisch und richtig.
Ausgehend von der Berechnung der Spielzüge können weitere Überlegungen hinsichtlich der Dauer des Umlegens angestellt werden. In diesem Sinne bietet die Aufgabe zusätzlich zum Problemlösen, Argumentieren, Kommunizieren und Darstellen auch die Möglichkeiten zum Modellieren. Es werden Vereinbarungen zur benötigten Zeit gemacht und zur dann zur Berechnung genutzt.
Für die in der Legende (vgl. unterrichtliche Ideen) beschriebene Ausgangssituation werden damit insgesamt 18 466 744 073 709 551 615 (ca. 18,5 Trillionen) Spielzüge benötigt. Verschieben die Priester im Tempel die Scheiben Tag und Nacht und benötigen dabei pro Zug 1 Sekunde, vergehen über 580 Milliarden Jahre bis der Turm komplett umgelegt wurde.
Hätten Sie mit diesem Ergebnis gerechnet?








