Mathematikerinnen und Mathematiker besuchen Ihre Schule

Computertomographie - wie Mathematik das Verborgene enthüllt

Vortragender:

Prof. Dr. Frank Werner

Zusammenfassung:

Wie funktioniert eigentlich ein Computertomograph? In diesem Vortrag wird zunächst anhand eines einfachen Beispiels einer Pralinenschachtel erklärt, wie man mittels
Röntgenstrahlen hineinsehen kann ohne sie zu öffnen. Die Mathematik spielt dabei eine sehr gewichtige Rolle. Was hierbei noch als kleine Knobelaufgabe gelöst werden kann, ist bei
einem modernen Computertomographen nicht per Hand möglich - dies muss ein Algorithmus übernehmen. Das dabei gelöste Problem wird als "Inverses Problem" bezeichnet, und heutzutage
existieren viele mögliche Lösungsverfahren. Dadurch wird deutlich, wie wichtig Mathematik in vielen Anwendungen und insbesondere der medizinischen Bildgebung heutzutage ist.

Goodstein-Folgen - schneller als jeder Beweis?

Vortragender:

Prof. Dr. Anton Freund

Zusammenfassung:

Wir studieren eine Folge von natürlichen Zahlen, die schnell ins Unendliche zu wachsen scheint (die ersten drei Zahlen haben 2, dann 13 und dann schon 154 Stellen). Tatsächlich landet die Folge irgendwann bei Null -- was aber wiederum nur mit Hilfe von "unendlichen Zahlen" bewiesen werden kann. Wir werden sehen, wie dies mit den Gödelschen Unvollständigkeitssätzen aus der mathematischen Logik zusammenhängt.

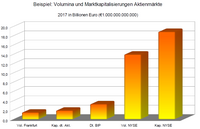
Profit ohne Risiko, Geld für umsonst - geht das?

Vortragender:

Prof. Dr. Tom Fischer

Zusammenfassung:

Auf der Suche nach einer Antwort werden anhand einfacher Beispiele wichtige Grundprinzipien der Finanzwelt illustriert:

• Warum, beispielsweise, können die Zinsen auf der anderen Seite des Atlantiks eine Rolle hier in Deutschland spielen? 
• Was haben Finanzmärkte zum einem mit Lotto und zum anderen mit fairen Spielen zu tun?
• Was kann es bedeuten, wenn eine Bank höhere Zinsen gibt als eine andere?
• Wieso bestimmt bei Aktien der Preis einer Kaufoption zugleich auch den Preis der zugehörigen Verkaufsoption?
• Und was ist eigentlich Finanzmathematik?

Absicht des Vortrags ist es, Einblicke in die Spielregeln des globalen Finanzcasinos und in die dahinter liegende Wissenschaft zu geben.

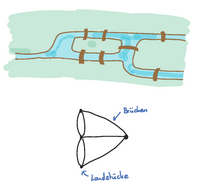
Das Königsberger Brückenproblem

Vortragende:

Prof. Dr. Madeleine Jotz

Zusammenfassung:

Die Stadt Königsberg wird durch den Pregel, einen Fluss, und seine zwei Inseln geteilt. Die beiden Stadthälften waren früher durch je drei Brücken mit den zwei Inseln verbunden. Die zwei Inseln waren untereinander durch eine weitere Brücke verbunden. Der Mathematiker Leonhard Euler bewies 1736 dass es keinen Weg gibt, bei dem man alle sieben Brücken genau einmal überquert. Die Methoden, die er dafür benutzte, und mit denen er das Problem deutlich vereinfachte, werden heute der "Graphentheorie" zugerechnet.

In diesem Vortrag werden wir sehen, wie dieses einfach zu formulierende, aber spannende Problem mit Hilfe der richtigen mathematischen Hilfsmitteln sehr leicht zu lösen wird.
 

Was hat Häkeln mit geometrischer Krümmung zu tun?

Vortragende:

Prof. Dr. Madeleine Jotz 

Zusammenfassung:

Dieser Vortrag erklärt, was es eigentlich heisst, wenn man sagt dass ein Objekt "gekrümmt" ist. Wir erklären insbesondere, wie eine Fläche aussieht, die sich überall "negativ" krümmt, und warum solche Flächen MathematikerInnen Jahrhunderte lang beschäftigt haben. Wir werden dann sehen, dass man erst vor etwa zwanzig Jahren gute Modelle für diese Flächen bekommen hat, als die Mathematikerin Daina Taimina feststellte, dass man sie einfach häkeln kann.

Was ist ein Punkt?

Vortragender:

Prof. Dr. Stefan Waldmann

Zusammenfassung:

Die scheinbar naive und unschuldig wirkende Frage wird als Startpunkt einer mehr als 3000-jährigen Wanderung durch die Mathematik und Physik der Geometrie genommen. Die Natur eines Punktes kann dabei von so vielen Blickwinkeln aus betrachtet werden, dass am Ende eine überraschend reichhaltige Einsicht in die Geometrie von Raum und Zeit entsteht. Die begonnene Reise von den Anfängen der Geometrie bis zu den neuen "punktlosen" Geometrien ist noch keineswegs zu einem Abschluss gekommen.

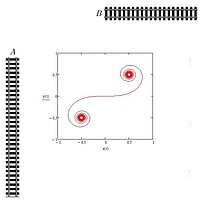
Wie verbindet man zwei Eisenbahnlinien, damit man möglichst angenehm darüber fahren kann?

Vortragende:

Prof. Dr. Sergey Dashkovskiy 

Zusammenfassung:

Betrachten wir zwei geradlinige Eisenbahnlinien, die auf zwei verschiedenen Geraden liegen (zum Beispiel so wie auf dem Bild).

Wie lassen sich diese zwei Strecken miteinander verbinden, sodass ein moderner Zug darüber fahren kann?

Die kürzeste Verbindung, die A und B durch eine gerade Strecke verbindet, ist nicht sinnvoll, weil der Zug dann darüber nicht fahren kann. Offensichtlich ist eine glatte Verbindung notwendig. Man kann eine kreisförmige Verbindung finden, die einen glatten Übergang liefert. Allerdings wird eine Fahrt darüber ziemlich unangenehm sein, da die zentrifugalen Kräfte sich sprunghaft ändern. Wir überlegen, wie man durch ein mathematisches Modell eine passende Verbindungskurve (Klothoide) entwerfen kann. Ausgehend von dem Begriff der Tangentialgeraden lernen wir etwas über die Krümmung einer Kurve und wie sie sich quantifizieren lässt. Dies hilft uns die gestellte Frage zu beantworten.

Wie entstehen Sterne, warum fliegt ein Flugzeug? Die Mathematik hilft zu verstehen.

Prof. Dr. Christian Klingenberg

Zusammenfassung:

Die zentrale Bedeutung der Mathematik für unsere Sicht auf die Welt wird illustriert an Beispielen aus Technik und Natur. U.a. werden wir eine große mit dem Computer berechnete Beschreibung der Entwicklung des Universums zeigen, bei der man sieht, wie aus den Anfangsstadien des Universums sich im Laufe der Zeit Sterne und Galaxien ausgebildet haben. Nur durch mathematische Theorien ist dies überhaupt möglich.

Paul Erdös und das Schubfachprinzip

Vortragender:

Dr. Jens Jordan

Zusammenfassung:

Paul Erdös - einen der bedeutendsten aber auch kuriosesten Mathematiker des 20. Jahrhunderts - war stets auf der Suche nach "schönen" beweisen. Einen schönen Beweis - welcher das Schubfachprinzip verwendet - werden wir uns genauer ansehen.

Hinweis: Besonders geeignet für die Oberstufe und für MathPlus-Kurse

Hasenplage in Pisa

Vortragender:

Dr. Jens Jordan

Zusammenfassung:

Die Fibonacci-Folge ist eine unendliche Folge von Zahlen, bei der die Summe zweier benachbarter Zahlen die unmittelbar folgende Zahl ergibt. Benannt ist sie nach Leonardo de Pisa, der damit im Jahr 1202 das Wachstum einer Kaninchenpopulation beschrieb. Im Vortrag wird diese Folge vorgestellt und Zusammenhänge zu Natur und Kunst dargelegt. Des Weiteren werden ein paar mathematische Eigenschaften der Fibonaccizahlen diskutiert. .

Hinweis: Diesen Vortrag gibt es in zwei Versionen. Eine Variante für die Unterstufe und eine für die Mittelstufe.

Wurstvermutung und Wurstkatastrophe

Vortragender:

Dr. Richard Greiner

Zusammenfassung:

Wie packt man 5, 50, 5000, 5.000.000 Kugeln möglichst effizient? Atome (und kugelförmige Moleküle) ordnen sich regelmäßig zu Kristallen an. Tatsächlich gibt es aber Überraschungen, denen wir im Vortrag auf die Schliche kommen. Benötigt werden hierzu geometrisches Grundwissen über einfache Flächenberechnungen (Kreis, Dreieck, Parallelogramm) und etwas räumliches Vorstellungsvermögen. Überlegungen, die in einem W-Seminar angestellt werden könnten, stehen neben harten Nüssen in der aktuellen Mathematischen Forschung. Dabei wird nicht nur sichtbar wie Mathematikerinnen und Mathematiker an der Uni arbeiten, sondern auch, warum scheinbar abstrakte Mathematik für technische Innovation verantwortlich ist.

Zielgruppe: ab Jgst 11.

A_15 - ein Kinderspiel

Vortragender:

Dr. Gunther Dirr

Zusammenfassung:

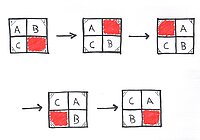
Der Vortrag behandelt einige mathematische Aspekte sogenannter "Schiebepuzzles". Anhand der konkreten Fragestellung, ob jede Ausgangskonfiguration in jede Endkonfiguration übergeführt werden kann, werden einfache Begriffe über Permutationsgruppen veranschaulicht. Am Ende des Vortrags liefert ein überraschend kurzer Beweis die Lösung der obigen Frage.

Der Vortrag ist für interessierte Schüler relativ unabhängig von ihrer mathematischen Vorbildung geeignet, da er nahezu ohne Schulmathematik auskommt. Durch diese "unkonventionelle" Art von Mathematik verblüfft er die meisten Zuhörer.

Wozu ist Mathematik, wozu sind Mathematikerinnen und Mathematiker nutze?

Vortragender:

PD Dr. Christian Zillober

Zusammenfassung:

"Mathematik ist ja schon interessant, aber was kann ich später damit anfangen?"

Wenn Sie sich diese Frage schon einmal gestellt haben und keine befriedigende Antwort bekommen haben, dann kann Ihnen dieser Vortrag weiterhelfen. Über verschiedene praktische Probleme wird Ihnen eine Idee dafür gegeben, wie mathematische Disziplinen wie etwa Optimierung, Statistik oder Kryptographie im Leben außerhalb von Schule und Universität angewendet werden können.

Außerdem wird vorgestellt, wie man in Würzburg Mathematik studieren kann.