Mathematicians visit your school
Are you interested in some math topic and you would like to receive a lecture at your school? Get an overview of our offer. Please fill out the registration form and send it back to us.
Profit ohne Risiko, Geld für umsonst - geht das?
Vortragender:
Prof. Dr. Tom Fischer
Zusammenfassung:
Auf der Suche nach einer Antwort werden anhand einfacher Beispiele wichtige Grundprinzipien der Finanzwelt illustriert:
- Warum, beispielsweise, können die Zinsen auf der anderen Seite des Atlantiks eine Rolle hier in Deutschland spielen?
- Was haben Finanzmärkte zum einem mit Lotto und zum anderen mit fairen Spielen zu tun?
- Was kann es bedeuten, wenn eine Bank höhere Zinsen gibt als eine andere?
- Wieso bestimmt bei Aktien der Preis einer Kaufoption zugleich auch den Preis der zugehörigen Verkaufsoption?
- Und was ist eigentlich Finanzmathematik?
Absicht des Vortrags ist es, Einblicke in die Spielregeln des globalen Finanzcasinos und in die dahinter liegende Wissenschaft zu geben.
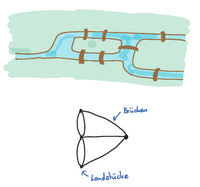
Das Königsberger Brückenproblem
Vortragende:
Prof. Dr. Madeleine Jotz
Zusammenfassung:
Die Stadt Königsberg wird durch den Pregel, einen Fluss, und seine zwei Inseln geteilt. Die beiden Stadthälften waren früher durch je drei Brücken mit den zwei Inseln verbunden. Die zwei Inseln waren untereinander durch eine weitere Brücke verbunden. Der Mathematiker Leonhard Euler bewies 1736 dass es keinen Weg gibt, bei dem man alle sieben Brücken genau einmal überquert. Die Methoden, die er dafür benutzte, und mit denen er das Problem deutlich vereinfachte, werden heute der "Graphentheorie" zugerechnet.
In diesem Vortrag werden wir sehen, wie dieses einfach zu formulierende, aber spannende Problem mit Hilfe der richtigen mathematischen Hilfsmitteln sehr leicht zu lösen wird.
Was hat Häkeln mit geometrischer Krümmung zu tun?
Vortragende:
Prof. Dr. Madeleine Jotz
Zusammenfassung:
Dieser Vortrag erklärt, was es eigentlich heisst, wenn man sagt dass ein Objekt "gekrümmt" ist. Wir erklären insbesondere, wie eine Fläche aussieht, die sich überall "negativ" krümmt, und warum solche Flächen MathematikerInnen Jahrhunderte lang beschäftigt haben. Wir werden dann sehen, dass man erst vor etwa zwanzig Jahren gute Modelle für diese Flächen bekommen hat, als die Mathematikerin Daina Taimina feststellte, dass man sie einfach häkeln kann.
Was ist ein Punkt?
Vortragender:
Prof. Dr. Stefan Waldmann
Zusammenfassung:
Die scheinbar naive und unschuldig wirkende Frage wird als Startpunkt einer mehr als 3000-jährigen Wanderung durch die Mathematik und Physik der Geometrie genommen. Die Natur eines Punktes kann dabei von so vielen Blickwinkeln aus betrachtet werden, dass am Ende eine überraschend reichhaltige Einsicht in die Geometrie von Raum und Zeit entsteht. Die begonnene Reise von den Anfängen der Geometrie bis zu den neuen "punktlosen" Geometrien ist noch keineswegs zu einem Abschluss gekommen.
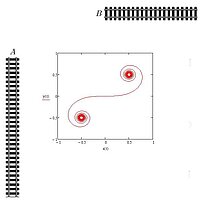
How do you connect two railway lines so that you can drive over them as pleasantly as possible?
Supervisor:
Prof. Dr. Sergey Dashkovskiy
Summary:
Let us take a look at two straight railroads that lie on two different lines (as in the picture).
How can these two routes be connected so that a modern train can travel over it?
The shortest link connecting A and B through a straight line does not make sense because the train cannot drive over it. Obviously, a smooth connection is required. One can find a circular connection that provides a smooth transition. However, a ride over it will be quite uncomfortable as the centrifugal forces change abruptly. We consider how to design a suitable connection curve (clothoid) by means of a mathematical model. Starting from the concept of tangential straight lines, we learn about the curvature of a curve and how it can be quantified. This helps us to answer this specific question.
How stars are made, why does an airplane fly? Mathematics helps to understand.
Lecturer:
Prof. Dr. Christian Klingenberg
Summary
The central importance of mathematics for our view of the world is illustrated by examples from technology and nature. We will show a suitable computer-simulated description of the evolution of the universe, showing how the initial stages of the universe have transformed stars and galaxies over time. This description is possible only through mathematical theories.
Paul Erdös and the drawer principle
Supervisor:
Dr. Jens Jordan
Summary:
Paul Erdös was one of the most important but also the most curious mathematicians of the 20th century. He was always looking for "beautiful evidences”. We will take a closer look about a nice proof which uses the drawer principle.
Rabbit plague in Pisa
Supervisor:
Dr. Jens Jordan
Summary
The Fibonacci sequence is an infinite sequence of numbers in which the sum of two adjacent numbers gives the immediately following number. It is named after Leonardo de Pisa, who described in 1202 the growth of a rabbit population. In the lecture, this sequence will be presented and connected to nature and art. Furthermore, a few mathematical properties of the Fibonacci numbers will be discussed.
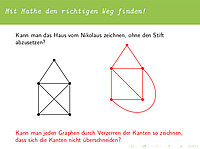
Find the right way with math
Supervisor:
Prof. Dr. Jörn Steuding
Summary:
How do I cheaply get from Würzburg to Berlin? How to organize efficient garbage collection? How do you behave in a labyrinth? Such everyday questions about orientation in complex environments can be treated with an interesting mix of mathematics and computer science. The concept of the graph allows a simplified representation of these problems (by reducing them to essential information) and allows clever algorithms to find solutions or at least strategies for dealing with them. The lecture should provide a first insight into mathematics at universities (especially graph theory) and in particular show that there are many interesting and often unresolved questions that are nevertheless easy to understand.
Sausage guess and sausage disaster
Supervisor:
Dr. Richard Greiner
Summary
How to pack 5, 50, 5000, 5,000,000 balls as mush efficiently as possible? Atoms (and globular molecules) regularly assemble into crystals. In fact, there are surprises that we come across in the lecture. This requires basic geometric knowledge about simple surface calculations (circle, triangle, parallelogram) and some spatial imagination. Considerations that could be made in a W seminar stand next to hard nuts in current mathematical research. It is not only visible how mathematicians work at the university, but also why seemingly abstract mathematics is responsible for technical innovation.
Target group: from grade 11.
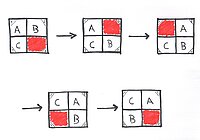
A_15 - a breeze
Supervisor:
Dr. Gunther Dirr
Summary
The lecture deals with some mathematical aspects of so-called "sliding puzzles". Based on the concrete question of whether each initial configuration can be transferred to each final configuration, simple terms about permutation groups are illustrated. At the end of the lecture, a surprisingly short proof provides the solution to the above question.
The lecture is suitable for interested students and it does not depend on their mathematical education, since it manages almost without school mathematics. This "unconventional" kind of mathematics amazes most listeners.
What is mathematics for, why are mathematicians used?
Supervisor:
PD Dr. Christian Zillober
Summary:
"Mathematics is interesting, but what can I do with it later?"
This lecture can help you, if you have asked yourself about this question and you did not receive a satisfactory answer. Various practical problems will give you an idea about how mathematical disciplines can be applied to life outside of school and university, such as optimization, statistics, or cryptography.
It also shows how to study mathematics in Würzburg.