Projekt Seilkamerasystem
Seilkamerasysteme ermöglichen es, Fernsehzuschauern noch näher am Geschehen, wie zum Beispiel bei Sportveranstaltungen, Konzerten, etc., zu sein, indem die Kamera über ein Seilsystem gesteuert die Protagonisten aus verschiedensten Blickwinkeln zeigt. Da die notwendigen Berechnungen der Seillängen über schulgeometrische Kenntnisse (Satz des Pythagoras oder Vektorrechnung) bestimmt werden können, ist die Entwicklung und Programmierung einer Steuerung für Kamerafahren aus mathematischer wie auch informatischer Sicht interessant. Im Rahmen der Schülerprojekttage des Lehrstuhls für Didaktik der Mathematik wurde ein Modell eines solchen Systems entwickelt und gebaut.
Das folgende Video zeigt die verschiedene Komponenten des Modells:
Materialien
Auf dieser Seite stellen wir weitere Materialien zur eigenen Umsetzung einer Spidercam als Projekt für den fächerübergreifenden Mathematik- und Informatikunterricht bereit. Dazu gehören:
Mit Materialien aus dem Baumarkt und etwas Elektronik lässt sich recht einfach ein Modell eines Seilkamerasystems herstellen. Dabei hängt ein Kameramodul an vier Schnüren, deren effektive Länge jeweils über eine von einem Schrittmotor getriebene Winde verändert werden kann.
Im Steuerprogramm müssen Seillängen und Differenzen ermittelt und in Motorumdrehungen umgerechnet werden: Um die Kamera von einem Startpunkt P1 zu einem gewünschten Zielpunkt P2 zu bewegen, werden für beide Punkte die jeweiligen Längen der vier Tragseile berechnet. Für jede der vier Schnüre ergibt sich somit eine Längendifferenz, die der zugehörige Schrittmotor entsprechend auf- oder abrollen muss. Zur informatischen Umsetzung der mathematischen Beziehungen auf einem MiniComputer (z. B. Raspberry Pi) eignen sich einfache, schulnahe Programmierumgebungen (z. B. Scratch) genauso wie höhere Sprachen (z. B. Python).
| Foto der Spidercam | Simluation der Spidercam in GeoGebra - ggb-Datei |
 | 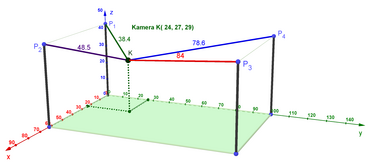 |
Die Berechnungen der Seillängen kann leicht entweder mithilfe des Satz des Pythagoras oder der Vektorrechnung erfolgen.
Erweiterungsmöglichkeiten: Vergleich verschiedener Wege
Bei konstanter gleicher Geschwindigkeit der Windenmotoren (grün) bewegt sich die Kamera nicht auf einer geradlinigen Verbindungslinie zwischen Start- und Zielpunkt. Dies bietet zahlreiche Möglichkeiten zur Vertiefung und Elaboration der verwendeten Methoden. Im ersten Video ist ein Vergleich zwischen der einfachen Methode und einer Möglichkeit, bei der die Geschwindigkeiten der Windenmotoren auf die größte Längenänderung normiert sind (blau), zu sehen. Wird der Pfad zwischen Start- und Zielpunkt mit Hilfe von Zwischenpunkten segmentiert ("Diskretisierung des Weges"), ergibt sich ein Verlauf, wie er im zweiten Video zu sehen ist. Nähere Informationen finden Sie hierzu auch in den zugehörigen Publikationen.
Um unser Modell der Spidercam nachzubauen, genügen bereits wenige Materialien aus dem Baumarkt und Elektrofachhandel. Hier finden Sie eine Materialliste zum Download.
Mit dem Programmcode in Python und Scratch stellen wir zwei Alternativen zur Programmierung der Spidercam dar.
Als Einstieg kann die Programmierung der Kamerasteuerung mittels der blockbasierten Programmiersprache Scratch. Scratch bietet dabei im Allgemeinen den Vorteil, dass Syntaxfehler durch „Zusammenstecken“ einzelner Programmierbausteine weitgehend vermieden werden. Deutlich performanter erfolgt die Programmierung allerdingsin einer höheren Programmiersprache; hier exemplarisch mit Python.
| Python | Scratch |
 | 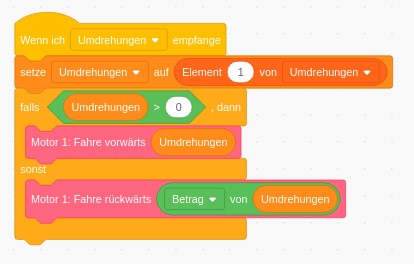 |
Downloads: | Downloads: Hinweis: Das Scratchprojekt nutzt die GPIO-Erweiterung für den RaspberryPi. Mehr Informationen dazu gibt es hier. Wir empfehlen Scratch lediglich für den Einstieg zu verwenden. Die Programmierung mit Python ist performanter und die Verwendung der Kamera kann ebenfalls leicht realisiert werden.
|
Zur Spidercam wurden bereits einige Artikel veröffentlicht:
Projektbericht Schülerprojekttage
Klöckner, V.; Siller, H.-S.; Adler, S. (2016). Wie bewegt sich eine Spidercam? Eine technische Errungenschaft, die nicht nur Fußballfans begeistert. Praxis der Mathematik 69 (58), S. 26–30
Günster, S. M. (2019). Modellierung einer Spidercam - ein Thema für Schule und Hochschule. in Borromeo Ferri, R., Greefrath, G. Günster, S. M. & Siller, H.-St.. ISTRON-Gruppe: Realitätsbezüge im Mathematikunterricht. in A. Frank, S. Krauss & K. Binder (Hrsg.), Beiträge zum Mathematikunterricht 2019. Münster: WTM-Verlag. S. 1307-1310. Link
Günster, S. M., Pöhner, N., Wörler, J. F. & Siller, H.-S. (im Druck). Mathematisches und informatisches Modellieren verbinden am Beispiel „Seilkamerasystem“. In Bracke, M., Ludwig, M. & Vorhölter, K. (Hrsg.), Neue Materialien für einen realitätsbezogenen Mathematikunterricht 7.
Günster, S. M., Pöhner, N., Wörler, J. F. & Siller, H.-S. (im Druck). Validierung beim mathe- und informatischen Modellieren – am Beispiel "Seilkamerasystem". in Beiträge zum Mathematikunterricht 2020.





