Schokoladenquadrate - Mathematische Hintergründe
Mathematischer Hintergrund zur Schokoladenaufgabe
Zur Lösung der Aufgabe werden die vorhandenen Quadrate systematisch abgezählt. Dabei ist es entscheidend, dass nicht nur die kleinen Quadrate gezählt werden, sondern einige dieser Felder zu größeren quadratischen Feldern zusammengefasst werden können (vgl. Mason, Burton & Stacey 2012).
Der Zusammenhang erschließt sich aus den Verknüpfung verschiedengroßer Schokoladentafeln. Dabei können die Muster und Strukturen erkannt und miteinander verknüpft werden.
Quadrate in einer 2•2 - Schokoladentafel
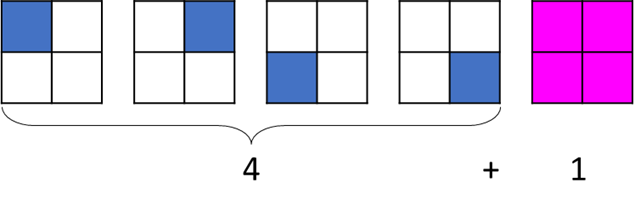
Die genaue Betrachtung der kleinen 2•2 - Schokoladentafel ist ausreichend, um zu erkennen, dass in dieser vier 1•1 - Quadrate (blau) und ein 2•2 - Quadrate (pink) zu finden sind.
Quadrate in einer 4•4 - Schokoladentafel
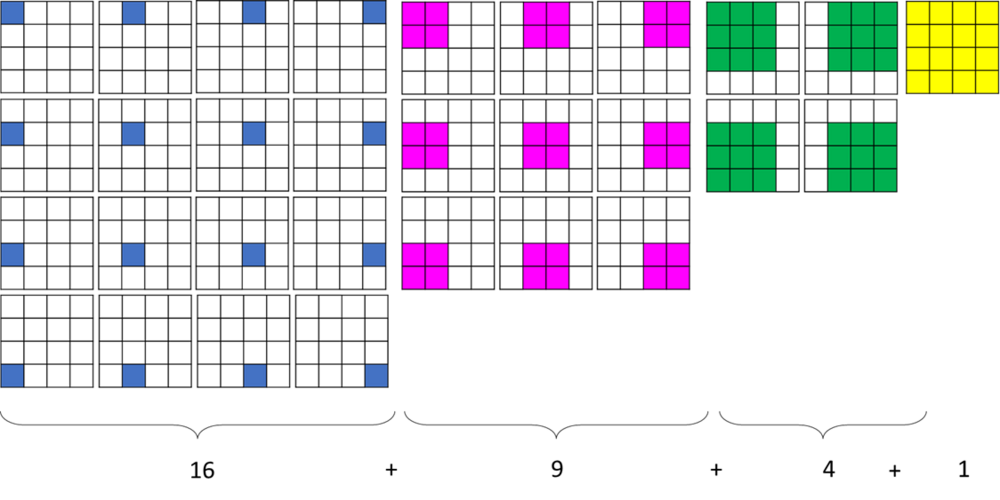
Hierbei werden nicht nur die kleinen 1•1 - Quadrate (blau) sowie das große 4•4 - Quadrat (gelb) betrachtet, sondern auch 2•2 - Quadrate (pink) und 3•3 - Quadrate (grün). Vorteilhaft ist es, die vorhanden Quadratvarianten systematisch festzuhalten.
Bei der Ermittlung der Anzahl der vorhandenen 2•2 - Quadrate ist zu berücksichtigen, dass diese nicht nur nebeneinander, sondern auch überlappend in das Quadrat gelegt werden. Das Auseinanderschneiden des Quadrates ist demnach keine hilfreiche Differenzierungsmaßnahme.
Durch Auszählen der beschrieben Quadrate ergibt sich die folgende Tabelle:

Eine alternative Vorgehensweise ist die Überlegung, wie viele 2•2 - Quadrate an die oberste Linie anstoßen. In unserem Fall sind das drei. Auch die nächst tiefere Linie wird (von unten) von drei Quadraten berührt. Die Systematik lässt sich fortführen. In unserem 4•4 - Quadrat lassen sich fünf waagrechte Linien erkennen, die unteren beiden werden allerdings nicht (von unten) durch die kleineren Quadrate berührt. Damit bleiben drei Linien übrig, die von jeweils drei Quadraten berührt werden. Dies ergibt insgesamt neun Möglichkeiten. Diese Idee lässt sich verallgemeinern:
Für die 4•4 - Schokoladentafel gilt (5 - K)•(5 - K) Quadrate vom Typ K•K.
Die Überlegungen können direkt auf die große Schokoladentafel mit 6•6 Quadraten übertragen werden:
Es gibt (7 - K)•(7 - K) Quadrate vom Typ K•K (vgl. Mason, Burton & Stacey 2012).
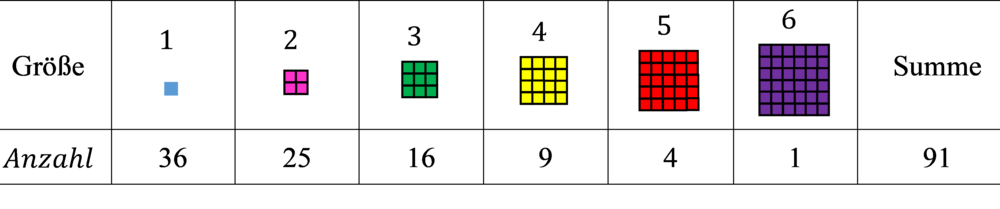
Die Erkenntnisse sind auf beliebig große Schokoladentafeln übertragbar. Jede Schokoladentafel hat N Zeilen und N Spalten. Damit gibt es insgesamt N + 1 waagrechte Linien, an die die Quadrate mit Seitenlänge K von unten angelegt werden. In jeder Schokoladentafel gibt es (N + 1 - K) Quadrate von Typ K•K in einer Reihe und damit ingesamt (N + 1 - K)•(N + 1 - K) = (N + 1 - K)2 Quadrate.
Die folgende Tabelle zeigt diese Überlegungen vereinfacht im Überblick:
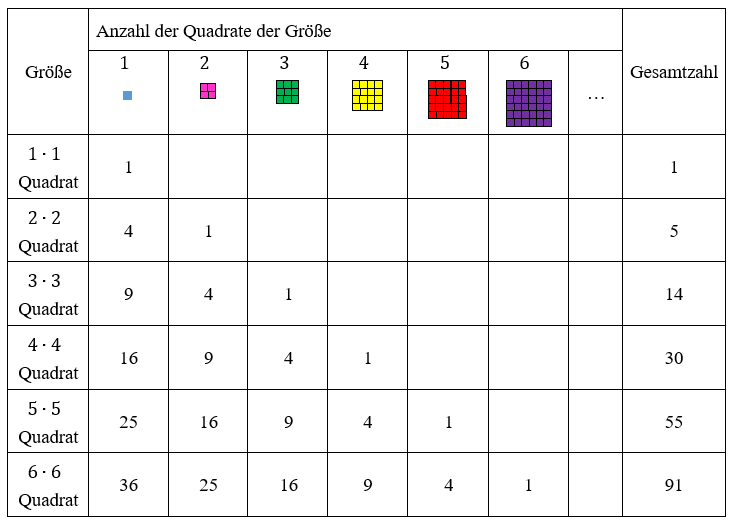
An dieser Tabelle wird deutlich, dass die Anzahl der Quadrate in den Schokoladentafeln durch die Summe der Quadratzahlen berechnen lässt. Die größte Zahl entspricht der Anzahl der 1•1 - Quadrate, in der Tabelle verschieben sich die Quadratzahlen also spaltenweise nach rechts.
Eine ganz andere Möglichkeit, die Anzahl der Möglichkeiten zu bestimmen, besteht darin, jeweils den Mittelpunkt der Teilquadrate einzufärben und im Quadrat zu markieren, wodurch die folgende Darstellung entsteht:
Dieses Vorgehen zeigt anschaulich die Entstehung der jeweils kleineren Quadrate. Probieren Sie selbst aus, was passiert, wenn Sie statt der Mittelpunkte die linke obere Ecke markieren. Richtig – auch dann können Sie die Folge der Quadratzahlen erkennen.
Alle diese Überlegungen führen letzendlich zu dem Schluss, dass die Anzahl der Quadrate in einer Schokoladentafel der Summe der Quadratzahlen entspricht. Sie lässt sich explizit mithilfe der folgenden Formel berechnen:
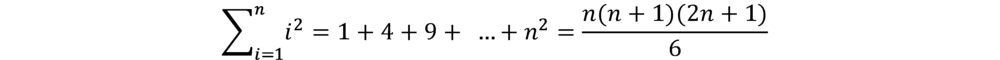
Literatur
Mason, J.; Burton, L.; Stacey, K. (20126): Mathematisch denken. Mathematik ist keine Hexerei. München: Oldenbourg Wissenschaftsverlag GmbH








